点 $P$ 和 $Q$ 在锐角三角形 $ABC$ 的边 $BC$ 上，满足 $\angle PAB=\angle BCA$ 且 $\angle CAQ=\angle ABC$．点 $M$ 和 $N$ 分别在直线 $AP$ 和 $AQ$ 上，使得 $P$ 是 $AM$ 的中点，且 $Q$ 是 $AN$ 的中点．证明：直线 $BM$ 和 $CN$ 的交点在三角形 $ABC$ 的外接圆上．（格鲁吉亚）
【难度】
【出处】
2014年第55届IMO试题
【标注】
【答案】
略
【解析】
如图，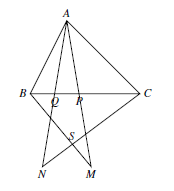
设 $S$ 是直线 $BM$ 和 $CN$ 的交点，记 $\beta =\angle QAC=\angle CBA$，
$\gamma =\angle PAB=\angle ACB$．由以上两式可得三角形 $ABP$ 和三角形 $CAQ$ 相似，因此
$
\dfrac{B P}{P M}=\dfrac{B P}{P A}=\dfrac{A Q}{Q C}=\dfrac{N Q}{Q C}
$
又由 $\angle BPM=\beta +\gamma =\angle CQN$ 知，三角形 $BPM$ 和三角形 $NQC$ 相似，故 $\angle BMP=\angle NCQ$，所以三角形 $BPM$ 和三角形 $BSC$ 也相似，从而有 $\angle CSB=\angle BPM=\beta+\gamma=180^{\circ}-\angle BAC$，得证．
设 $S$ 是直线 $BM$ 和 $CN$ 的交点，记 $\beta =\angle QAC=\angle CBA$，$\gamma =\angle PAB=\angle ACB$．由以上两式可得三角形 $ABP$ 和三角形 $CAQ$ 相似，因此
$
\dfrac{B P}{P M}=\dfrac{B P}{P A}=\dfrac{A Q}{Q C}=\dfrac{N Q}{Q C}
$
又由 $\angle BPM=\beta +\gamma =\angle CQN$ 知，三角形 $BPM$ 和三角形 $NQC$ 相似，故 $\angle BMP=\angle NCQ$，所以三角形 $BPM$ 和三角形 $BSC$ 也相似，从而有 $\angle CSB=\angle BPM=\beta+\gamma=180^{\circ}-\angle BAC$，得证．
答案
解析
备注
