设 $n\geqslant 3$ 为整数，$\Gamma_1,\Gamma_2,\cdots,\Gamma_m$ 为平面上半径为 $1$ 的圆，圆心分别为 $O_1,O_2,\cdots,O_n$，假设任一直线至多和两个圆相交或相切．求证：$\displaystyle \sum\limits_{1\leqslant i<j\leqslant n}{\dfrac{1}{{{O}_{i}}{{O}_{j}}}}\leqslant \frac{(n-1)\pi }{4}$．（乌克兰）
【难度】
【出处】
2002年第43届IMO试题
【标注】
【答案】
略
【解析】
记 $O_1,O_2,\cdots,O_n$ 构成的点集为 $A$．先证一个引理．
引理：$O_i,O_j,O_k$ 是 $A$ 中任意三点，设 $\angle O_iO_jO_k=\theta$，则 $\dfrac{1}{{O}_{i}{{O}_{j}}}\leqslant \dfrac{\theta}{2}$．
证明如下，如图
作中位线 $l$，则 $O_i,O_j,O_k$ 至 $l$ 的距离大于 $1$，于是 $O_j$ 至 $O_iO_k$ 的距离大于 $2$，或 $O_iO_j\sin\theta>2$，故 $\dfrac{1}{{O}_{i}{{O}_{j}}}<\dfrac{\sin\theta}{2}<\dfrac{\theta}{2}$．（弧度制）
为了论述方便，我们可把引理改成更对称形式，即 $\dfrac{1}{O_iO_j}+\dfrac{1}{O_iO_k}<\theta$．
下面我们来证明结论．
设 $A$ 的凸包为 $P_1P_2\cdots P_m$，内点为 $Q_1,Q_2,\cdots,Q_l$，于是 $m+l=n$．
先研究 $\displaystyle \sum\limits_i\dfrac{1}{P_iQ_j}$，其中 $P_i$ 是固定一点，$O_j$ 跑遍 $A$ 中元素，除了 $P_i$．
易知所有射线 $P_iO_j$ "挤"在一个夹角（设为 $\alpha$）小于 $\pi $ 的角内，分成 $n-2$ 个不相交的角，于是由引理，有
$\displaystyle 2\sum\limits_i\dfrac{1}{P_iQ_j}<\alpha +\dfrac{\beta+\gamma}{2}$ ①
$\beta,\gamma$ 是"最靠边"的两个角．
再考虑任一内点 $Q_i$，这里需要一点技巧．对于 $A$ 中任一点 $O_j(\ne Q_i)$，引进它关于 $Q_i$ 的对称点，这样一共得到 $2n-2$ 个点，其中一半属于 $A$，一半不属于 $A$．
于是分成和为 $2\pi$ 的 $2n-2$ 个角，对应的 $2n-2$ 个点依次为 $O_1^\prime,O_2^\prime,\cdots,O_{2n-2}^\prime$．
现考虑"相邻"两点 $O_k^\prime$ 和 $O_{k+1}^\prime$，设 $\angle O_k^\prime Q_iO_{k+1}^\prime=\theta$．
若 $O_k^\prime,O_{k+1}^\prime\in A$ 或 $O_k^\prime,O_{k+1}^\prime\not\in A$，显然有
$\dfrac{1}{Q_iO_k^\prime}+\dfrac{1}{Q_iO_{k+1}^\prime}<\theta$，
若 $O_k^\prime,O_{k+1}^\prime$ 之一属于 $A$，另一不属于 $A$，比方说 $O_{k+1}^\prime\not\in A$，则它关于 $Q_i$ 的对称点 $O_{k+1}^{\prime\prime}\in A$，此时如图．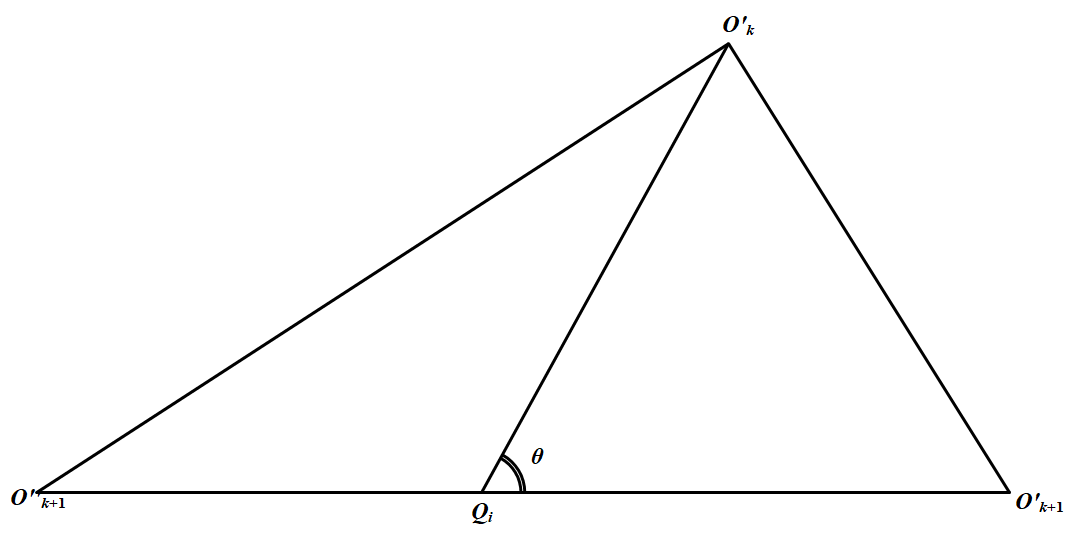
考虑 $O_k^\prime$ 至 $Q_iO_{k+1}^\prime$ 距离和 $O^\prime_{k+1}$ 至 $Q_iO^\prime_k$ 距离，它们均为 $\triangle O_k^\prime Q_i O^{\prime\prime}_{k+1}$ 中的高长，故大于 $2$，于是由引理 $\dfrac{1}{O_k^\prime Q_i}+\dfrac{1}{O_{k+1}^\prime Q_i}<\theta$．
然后求和，考虑有一半边是"引进"的，故
$\displaystyle \sum\limits_i\dfrac{1}{Q_iO_j^\prime}<\dfrac{2\pi}{4}=\dfrac{\pi}{2}$ ②
结合 ① 与 ②，有
$\displaystyle \begin{aligned}
\sum_{i,j}\frac{1}{O_iO_j}=&\sum_i\sum_j\dfrac{1}{P_iO_j}+\sum_i\sum_j\dfrac{1}{Q_iO^\prime_j}\\
&<\frac{1}{2}\left(\frac{1}{2}\sum\alpha+\frac{1}{4}\sum(\beta+\gamma)+\frac{\pi}{2}l\right)\\
&\leqslant \frac{1}{2}[\frac{1}{2}(m-2)\pi+\frac{\pi}{2}+\frac{\pi}{2}l]\\
&=\frac{n-1}{4}\pi
\end{aligned}$
其中外面的系数 $\dfrac{1}{2}$ 是由于每条边 $O_iO_j$ 被计两次．而当只有凸 $m$ 边形时 $\displaystyle \sum(\beta+\gamma)=2\pi(m\geqslant 4)$ 或 $\pi(m=3)$，一加内点便可能小于．
引理：$O_i,O_j,O_k$ 是 $A$ 中任意三点，设 $\angle O_iO_jO_k=\theta$，则 $\dfrac{1}{{O}_{i}{{O}_{j}}}\leqslant \dfrac{\theta}{2}$．
证明如下，如图
作中位线 $l$，则 $O_i,O_j,O_k$ 至 $l$ 的距离大于 $1$，于是 $O_j$ 至 $O_iO_k$ 的距离大于 $2$，或 $O_iO_j\sin\theta>2$，故 $\dfrac{1}{{O}_{i}{{O}_{j}}}<\dfrac{\sin\theta}{2}<\dfrac{\theta}{2}$．（弧度制）为了论述方便，我们可把引理改成更对称形式，即 $\dfrac{1}{O_iO_j}+\dfrac{1}{O_iO_k}<\theta$．
下面我们来证明结论．
设 $A$ 的凸包为 $P_1P_2\cdots P_m$，内点为 $Q_1,Q_2,\cdots,Q_l$，于是 $m+l=n$．
先研究 $\displaystyle \sum\limits_i\dfrac{1}{P_iQ_j}$，其中 $P_i$ 是固定一点，$O_j$ 跑遍 $A$ 中元素，除了 $P_i$．
易知所有射线 $P_iO_j$ "挤"在一个夹角（设为 $\alpha$）小于 $\pi $ 的角内，分成 $n-2$ 个不相交的角，于是由引理，有
$\displaystyle 2\sum\limits_i\dfrac{1}{P_iQ_j}<\alpha +\dfrac{\beta+\gamma}{2}$ ①
$\beta,\gamma$ 是"最靠边"的两个角．
再考虑任一内点 $Q_i$，这里需要一点技巧．对于 $A$ 中任一点 $O_j(\ne Q_i)$，引进它关于 $Q_i$ 的对称点，这样一共得到 $2n-2$ 个点，其中一半属于 $A$，一半不属于 $A$．
于是分成和为 $2\pi$ 的 $2n-2$ 个角，对应的 $2n-2$ 个点依次为 $O_1^\prime,O_2^\prime,\cdots,O_{2n-2}^\prime$．
现考虑"相邻"两点 $O_k^\prime$ 和 $O_{k+1}^\prime$，设 $\angle O_k^\prime Q_iO_{k+1}^\prime=\theta$．
若 $O_k^\prime,O_{k+1}^\prime\in A$ 或 $O_k^\prime,O_{k+1}^\prime\not\in A$，显然有
$\dfrac{1}{Q_iO_k^\prime}+\dfrac{1}{Q_iO_{k+1}^\prime}<\theta$，
若 $O_k^\prime,O_{k+1}^\prime$ 之一属于 $A$，另一不属于 $A$，比方说 $O_{k+1}^\prime\not\in A$，则它关于 $Q_i$ 的对称点 $O_{k+1}^{\prime\prime}\in A$，此时如图．
考虑 $O_k^\prime$ 至 $Q_iO_{k+1}^\prime$ 距离和 $O^\prime_{k+1}$ 至 $Q_iO^\prime_k$ 距离，它们均为 $\triangle O_k^\prime Q_i O^{\prime\prime}_{k+1}$ 中的高长，故大于 $2$，于是由引理 $\dfrac{1}{O_k^\prime Q_i}+\dfrac{1}{O_{k+1}^\prime Q_i}<\theta$．然后求和，考虑有一半边是"引进"的，故
$\displaystyle \sum\limits_i\dfrac{1}{Q_iO_j^\prime}<\dfrac{2\pi}{4}=\dfrac{\pi}{2}$ ②
结合 ① 与 ②，有
$\displaystyle \begin{aligned}
\sum_{i,j}\frac{1}{O_iO_j}=&\sum_i\sum_j\dfrac{1}{P_iO_j}+\sum_i\sum_j\dfrac{1}{Q_iO^\prime_j}\\
&<\frac{1}{2}\left(\frac{1}{2}\sum\alpha+\frac{1}{4}\sum(\beta+\gamma)+\frac{\pi}{2}l\right)\\
&\leqslant \frac{1}{2}[\frac{1}{2}(m-2)\pi+\frac{\pi}{2}+\frac{\pi}{2}l]\\
&=\frac{n-1}{4}\pi
\end{aligned}$
其中外面的系数 $\dfrac{1}{2}$ 是由于每条边 $O_iO_j$ 被计两次．而当只有凸 $m$ 边形时 $\displaystyle \sum(\beta+\gamma)=2\pi(m\geqslant 4)$ 或 $\pi(m=3)$，一加内点便可能小于．
答案
解析
备注
