2001年第42届IMO试题

• 知识点

  >

  二试组合部分

略

先列出一个 $21$ 行 $20$ 列的表格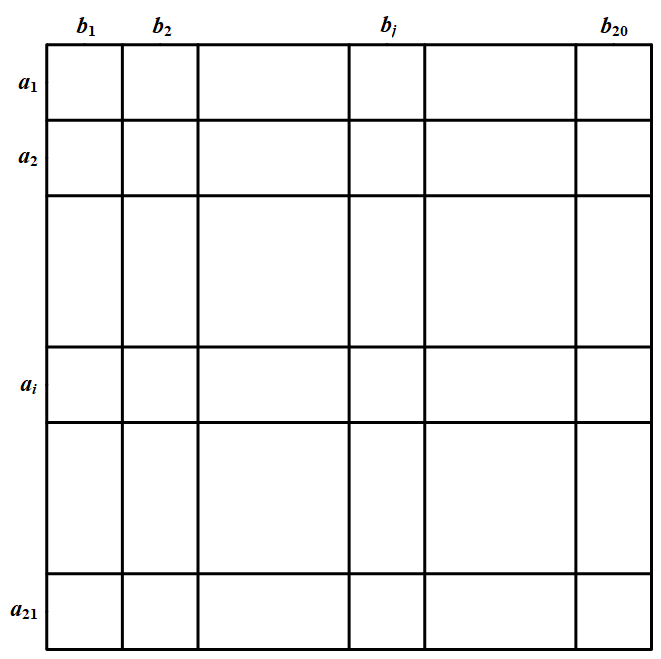．在第 $i$ 行，第 $j$ 列 $(1\leqslant i\leqslant 21,1\leqslant j\leqslant 20,i,j\in\mathbb{Z})$ 的格内填上第 $i$ 个女孩和第 $j$ 个男孩共同答出题目的题号（若有不少于 $2$ 个共同答出的题目，任选一个即可）．
因为每个男孩至多答对 $6$ 题，所以每一个列上至多有 $6$ 个不一样的题号．对这列的每一格，若填上的题号在这列出现不少于 $3$ 次，则打上蓝圈，因此，对每一种题号，要么都打蓝圈，要么都不打．由抽屉原理，至少有一种题号不少于 $\left(\left[\dfrac{21}{6}\right]+1=\right)4$ 个，所以必有蓝圈．
若蓝圈不多于 $10$ 个，则至少剩下 $11$ 格没打蓝圈．因为有一种题号已被打上蓝圈，所以至少剩下 $5$ 种题号没打蓝圈，因此其中至少有一种题号出现不少于 $\left[\dfrac{11}{5}\right]+1=3$ 个，应打蓝圈，矛盾．所以每一列至少有 $11$ 个蓝圈，整个表格至少有 $(11\times 20=)220$ 个蓝圈．
因为每个女孩至多答对 $6$ 题，所以每一行也至多有 $6$ 个不一样的题号．对这行的每一格，若填上的题号在这行出现不少于 $3$ 次，则打上红圈．同理可得每一行至少有 $10$ 个红圈，整个表格至少有 $(10\times 21=)210$ 个红圈．
又因为此表格共有 $(21\times 20=)420$ 格，而 $220+210=430>420$．所以至少有一格被同时打上红圈和蓝圈，设这格所填题号为 $M$，对这格所在的列来说，至少有 $3$ 格填的是 $M$，设它们所在行为第 $a_1,a_2,a_3$ 行；则这格所在的行来说，至少有 $3$ 格填的是 $M$，设它们所在列为第 $b_1,b_2,b_3$ 列．因此第 $a_1,a_2,a_3$ 名女孩和第 $b_1,b_2,b_3$ 名男孩同时答对题号为 $M$ 的题目．
所以有一道题，至少被 $3$ 个女孩和 $3$ 个男孩解出．