在 $\triangle ABC$ 中，$AP$ 平分 $\angle BAC$，交 $BC$ 于 $P$，令 $BQ$ 平分 $\angle ABC$，交 $CA$ 于 $Q$，已知 $\angle BAC=60^\circ,AB+BP=AQ+QB$，问 $\triangle ABC$ 的各角的角的度数可能值是多少？（以色列）
【难度】
【出处】
2001年第42届IMO试题
【标注】
【答案】
略
【解析】
如图，延长 $AB$ 至 $E$，使 $BP=BE$．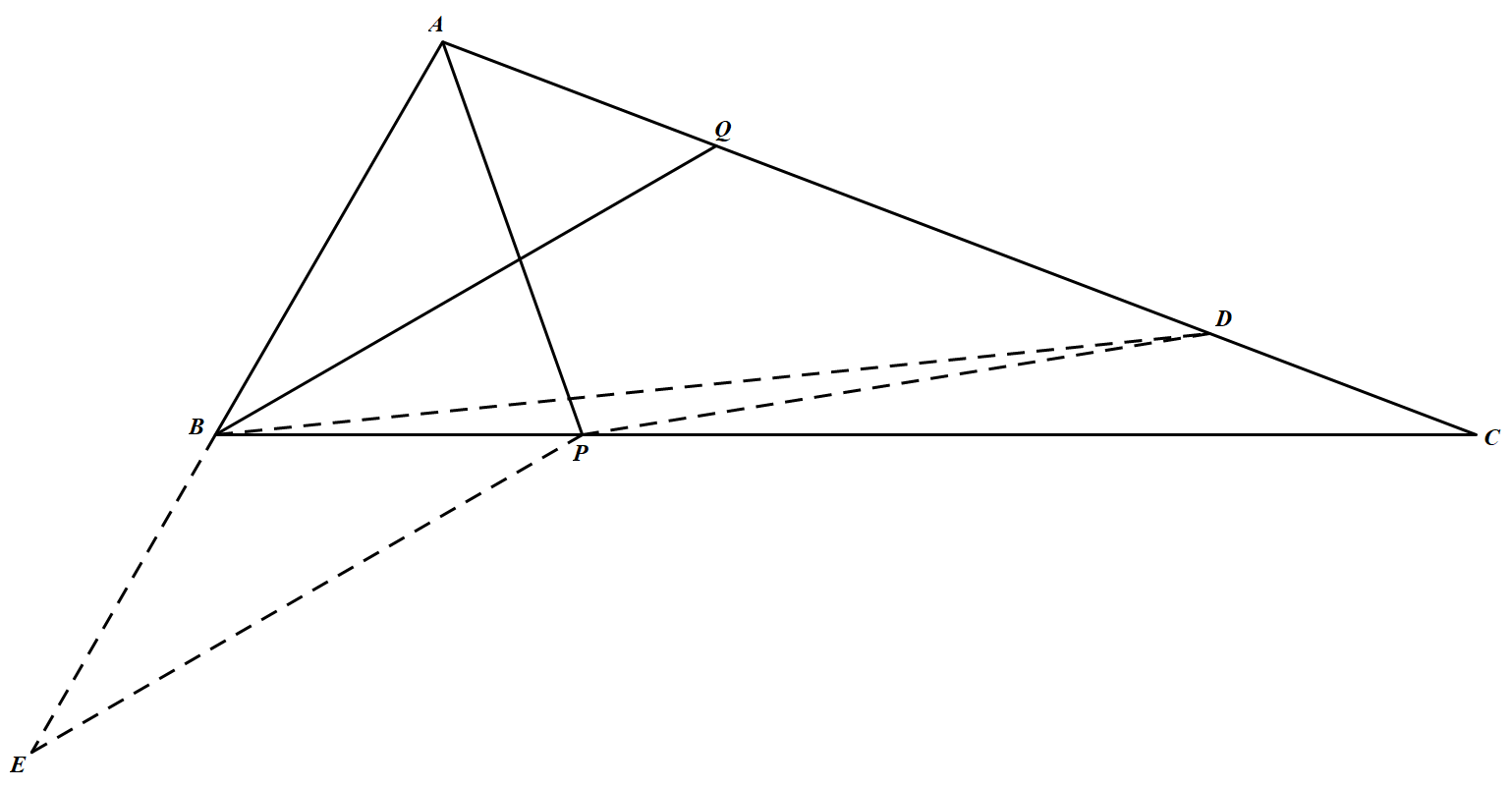
记 $\angle ABC=\angle B,\angle ACB=\angle C$．
今在 $AC$ 或延长线上找一点 $D$，使 $AD=AE$，则由条件知 $QD=QB$．
由于 $\triangle APD\cong\triangle APE$，故 $\angle ADP=\angle E=\dfrac{1}{2}\angle B$，而
$\begin{aligned}
\angle QDB&=\dfrac{1}{2}\angle AQB\\
&=\frac{1}{2}(\angle QBC+\angle C)\\
&=\frac{1}{4}\angle B+\angle C
\end{aligned}$
下面分情况讨论．
（1）当 $C$ 与 $D$ 重合时，有 $\angle B=80^\circ,\angle C=40^\circ$，容易验证此时确实满足 $AB+BP=AC=AQ+QB$．
（2）当 $D$ 在 $CQ$ 内时，有
$\begin{aligned}
\angle BDP&=\angle ADP-\angle ADB\\
&=\frac{1}{2}\angle B-\left(\frac{1}{4}\angle B+\frac{1}{2}\angle C\right)\\
&=\frac{1}{4}\angle B=\frac{1}{2}\angle C
\end{aligned}$
而此时还有
$\begin{aligned}
\angle DPC&=\angle ADP-\angle C\\
&=\frac{1}{2}\angle B-\angle C\\
&=2\angle BDP
\end{aligned}$
于是 $BP=DP$．
对 $\triangle ABP$ 和 $\triangle ADP$ 分别用正弦定理，得 $\sin\angle B=\sin\angle ADP$．
由于 $AD=AB+BP>AB,\angle B=\angle ADP$ 是不可能的，于是 $A,B,P,D$ 共圆，故 $\angle DPC=60^\circ$
此即 $\dfrac{1}{2}\angle B-\angle C=60^\circ$
又 $\angle B+\angle C=120^\circ$
得 $\angle C=0^\circ$，不可能．
（3）当 $D$ 在 $AC$ 延长线上时，同理仍有 $PD=BP$，可知 $A,B,P,D$ 共圆，但 $P$ 在 $\triangle ABD$ 内部，不可能．
综上所述，只能有 $\angle B=80^\circ,\angle C=40^\circ$．
记 $\angle ABC=\angle B,\angle ACB=\angle C$．今在 $AC$ 或延长线上找一点 $D$，使 $AD=AE$，则由条件知 $QD=QB$．
由于 $\triangle APD\cong\triangle APE$，故 $\angle ADP=\angle E=\dfrac{1}{2}\angle B$，而
$\begin{aligned}
\angle QDB&=\dfrac{1}{2}\angle AQB\\
&=\frac{1}{2}(\angle QBC+\angle C)\\
&=\frac{1}{4}\angle B+\angle C
\end{aligned}$
下面分情况讨论．
（1）当 $C$ 与 $D$ 重合时，有 $\angle B=80^\circ,\angle C=40^\circ$，容易验证此时确实满足 $AB+BP=AC=AQ+QB$．
（2）当 $D$ 在 $CQ$ 内时，有
$\begin{aligned}
\angle BDP&=\angle ADP-\angle ADB\\
&=\frac{1}{2}\angle B-\left(\frac{1}{4}\angle B+\frac{1}{2}\angle C\right)\\
&=\frac{1}{4}\angle B=\frac{1}{2}\angle C
\end{aligned}$
而此时还有
$\begin{aligned}
\angle DPC&=\angle ADP-\angle C\\
&=\frac{1}{2}\angle B-\angle C\\
&=2\angle BDP
\end{aligned}$
于是 $BP=DP$．
对 $\triangle ABP$ 和 $\triangle ADP$ 分别用正弦定理，得 $\sin\angle B=\sin\angle ADP$．
由于 $AD=AB+BP>AB,\angle B=\angle ADP$ 是不可能的，于是 $A,B,P,D$ 共圆，故 $\angle DPC=60^\circ$
此即 $\dfrac{1}{2}\angle B-\angle C=60^\circ$
又 $\angle B+\angle C=120^\circ$
得 $\angle C=0^\circ$，不可能．
（3）当 $D$ 在 $AC$ 延长线上时，同理仍有 $PD=BP$，可知 $A,B,P,D$ 共圆，但 $P$ 在 $\triangle ABD$ 内部，不可能．
综上所述，只能有 $\angle B=80^\circ,\angle C=40^\circ$．
答案
解析
备注
