圆 $\Gamma_1$ 和圆 $\Gamma_2$ 相交于点 $M$ 和 $N$．设 $l$ 是圆 $\Gamma_1$ 和圆 $\Gamma_2$ 的两条公切线中距离 $M$ 较近的那条公切线．$l$ 与圆 $\Gamma_1$ 相切于点 $A$，与圆 $\Gamma_2$ 相切于点 $B$．设经过点 $M$ 且与 $l$ 平行的直线与圆 $\Gamma_1$ 还相交于点 $C$，与圆 $\Gamma_2$ 还相交于点 $D$．直线于 $CA$ 和 $DB$ 相交于点 $E$，直线 $AN$ 和 $CD$ 相交于点 $P$．直线 $BN$ 和 $CD$ 相交于点 $Q$．求证 $EP=EQ$．（俄罗斯）
【难度】
【出处】
2000年第41届IMO试题
【标注】
【答案】
略
【解析】
如图，联结 $NM$ 并延长后交 $AB$ 于 $R$，联结 $EM,AM$ 和 $BM$．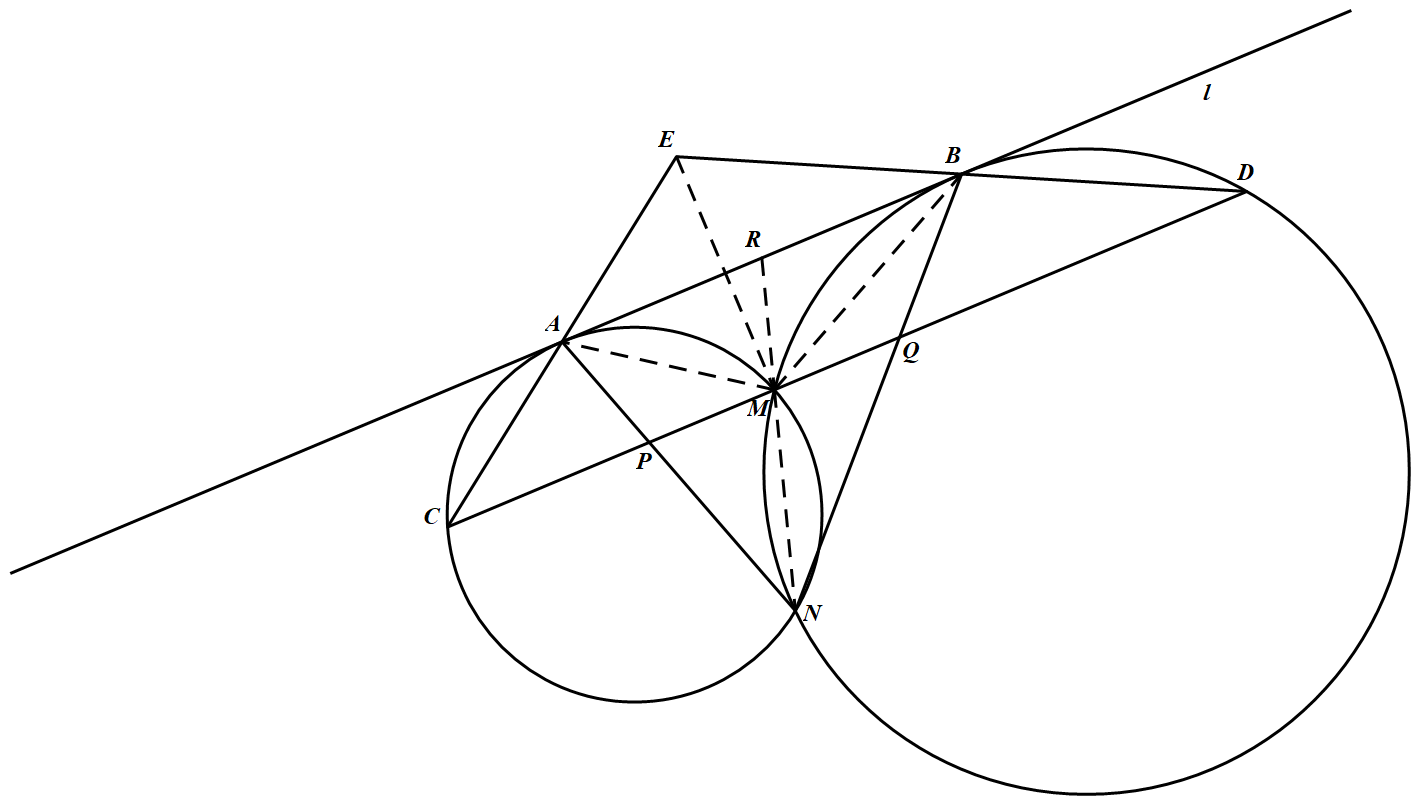
由于 $AR^2=RM\cdot RN=RB^2$．
故 $AR=RB$，又 $PQ\parallel AB$，故 $PM=MQ$．如果我们还能证明 $EM\perp PQ$，则 $EM$ 是 $PQ$ 之中垂线，$EP=EQ$ 就成立了．
下面就证明 $EM\perp PQ$，也即证明 $EM\perp AB$．
由于 $\angle EAB=\angle ECQ=\angle MAB$
同理可证 $\angle ABE=\angle ABM$
由此可知 $AB$ 垂直平分 $EM$．
由于 $AR^2=RM\cdot RN=RB^2$．故 $AR=RB$，又 $PQ\parallel AB$，故 $PM=MQ$．如果我们还能证明 $EM\perp PQ$，则 $EM$ 是 $PQ$ 之中垂线，$EP=EQ$ 就成立了．
下面就证明 $EM\perp PQ$，也即证明 $EM\perp AB$．
由于 $\angle EAB=\angle ECQ=\angle MAB$
同理可证 $\angle ABE=\angle ABM$
由此可知 $AB$ 垂直平分 $EM$．
答案
解析
备注
