设 $A{H}_{1},B{H}_{2},C{H}_{3}$ 是锐角 $\triangle ABC$ 的三条高．$\triangle ABC$ 的内切圆与边 $BC,CA,AB$ 分别相切与点 $T_1,T_2,T_3$．设直线 $l_1,l_2,l_3$ 分别是直线 $H_2H_3,H_3H_1,H_1H_2$ 关于直线 $T_2T_3,T_3T_1,T_1T_2$ 的对称直线．求证：$l_1,l_2,l_3$ 所确定的三角形其顶点都在 $\triangle ABC$ 的内切圆上．（俄罗斯）
【难度】
【出处】
2000年第41届IMO试题
【标注】
【答案】
略
【解析】
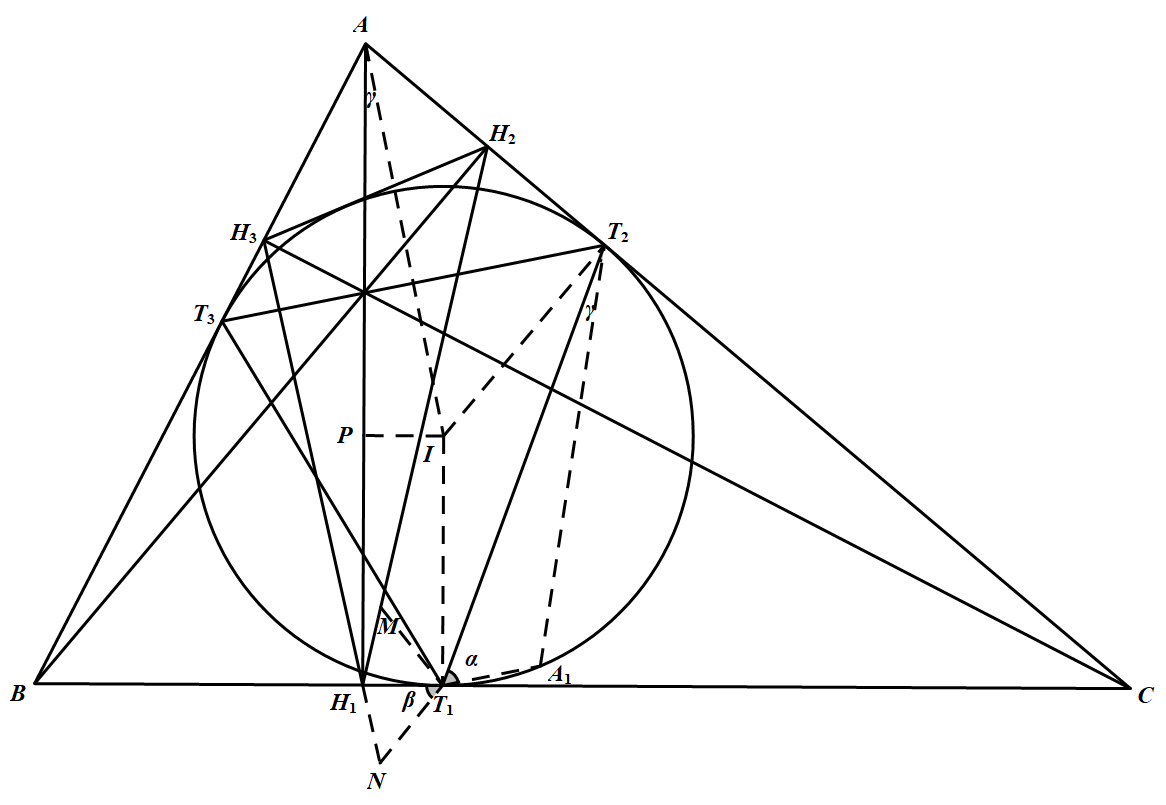如图，不妨设 $\angle B\geqslant\angle C$（分别记 $\angle A,\angle B,\angle C$ 为 $\angle BAC,\angle ABC$ 和 $\angle ACB$）．我们的证明方法如下：在内切圆 $I$（$I$ 是 $\triangle ABC$ 之内心）上确确实实找到一点，这一点关于 $T_1T_3$ 的对称点在 $H_1H_3$ 上，而关于 $T_1T_2$ 的对称点在 $H_1H_2$ 上，或者说这等价于证明了 $l_2,l_3$ 的交点在 $\odot I$ 上，其余两个交点也就同理可证了．
如图，我们用分析的方法首先假定该点 $A_1$ 已经找到，于是，在直线 $H_3H_1$ 及 $H_2H_1$ 上必存在点 $N$ 和 $M$，满足 $NT_1=MT_1=T_1A_1$ 及 $\angle NT_1T_3=\angle A_1T_1T_3,\angle MT_1T_2=\angle A_1T_1T_2$．
由于 $\angle MH_1T_1=\angle NH_1T_1=\angle H_3H_1B=\angle A$，又 $MT_1=NT_1$ 及 $H_1T_1$ 为公共边，我们猜测可能有 $\triangle MH_1T_1\cong\triangle NH_1T_1$，于是令 $\angle MT_1H_1=\angle NT_1H_1=\beta$，令 $\angle T_2T_1A_1=\alpha$，如图所示．
由条件知：
$\begin{aligned}
\beta+90^\circ-\frac{\angle B}{2}&=\angle T_3T_1N=\angle T_3T_1A_1\\
&=\angle T_3T_1T_2+\alpha\\
&=90^\circ-\frac{\angle A}{2}+\alpha\\
&=90^\circ-\frac{\angle A}{2}+\angle MT_1T_2\\
&=90^\circ-\frac{\angle A}{2}+\angle H_1T_1T_2-\beta\\
&=180^\circ+\frac{\angle C-\angle A}{2}-\beta\end{aligned}$
故 $\beta=90^\circ-\dfrac{1}{2}\angle A,\alpha=90^\circ-\dfrac{1}{2}\angle B$，
所以 $\triangle H_1T_1N$ 是等腰三角形，而
$\begin{aligned}
\angle T_3T_1A_1&=\angle T_3T_1T_2+\alpha\\
&=90^\circ-\frac{1}{2}\angle A+90^\circ-\frac{1}{2}\angle B\\
&=90^\circ+\frac{1}{2}\angle C\\
&=180^\circ-\left(90^\circ-\frac{1}{2}\angle C\right)\\
&=180^\circ-\angle T_1T_3T_2
\end{aligned}$
故 $T_1A_1\parallel T_3T_2$．
于是，我们这样作 $M,N$，及 $A_1$，延长 $H_3H_1$ 至 $N$，使 $H_1N=H_1T_1$，作 $N$ 关于 $BC$ 的对称点 $M$，其必在直线 $H_1H_2$ 上．又作等腰梯形 $T_3T_1A_1T_2$，由前面的分析，知 $\angle NT_1T_3=\angle A_1T_1T_3$ 及 $\angle MT_1T_2=\angle A_1T_1T_2$ 都保证了，$MT_1=NT_1$ 也显然，接下来唯一要做的事就是证明 $NT_1=A_1T_1$ 了．
易知
$\begin{aligned}
\angle T_1T_2A_1&=\angle T_1T_3T_2-\angle T_1T_2T_3\\
&=90\circ-\frac{1}{2}\angle C-\left(90^\circ-\frac{1}{2}\angle B\right)\\
&=\frac{1}{2}(\angle B-\angle C)\\
&=\frac{1}{2}\angle A-(90^\circ-\angle B)\\
&=\angle IAH_1\triangleq\gamma
\end{aligned}$
作 $IP\perp AH_1$，$P$ 是垂足，由 $\triangle H_1T_1N\sim\triangle AT_3T_2$，知
$\begin{aligned}
\frac{NT_1}{T_2T_3}&=\frac{H_1T_1}{AT_2}=\frac{PI}{AT_2}\\
&=\frac{AI\sin\gamma}{AI\sin\angle AIT_2}=\frac{\sin\gamma}{\sin\angle AT_2T_3}\\
&=\frac{\sin\gamma}{\sin\angle AT_2T_3}=\frac{A_1T_1}{T_2T_3}
\end{aligned}$
故 $NT_1=A_1T_1$．
于是命题证毕．
答案
解析
备注
