设 $n$ 是一个固定的正偶数．考虑一块 $n×n$ 的正方板，它被分成 ${n}^{2}$ 个单位正方格．板上两个不同的正方格如果有一条公共边，就称它们为相邻的．
将板上 $N$ 个单位正方格作上标记，使得板上的任意正方格（作上标记的或者没有作上标记的）都与至少一个作上标记的正方格相邻．
确定 $N$ 的最小值．（白俄罗斯）
将板上 $N$ 个单位正方格作上标记，使得板上的任意正方格（作上标记的或者没有作上标记的）都与至少一个作上标记的正方格相邻．
确定 $N$ 的最小值．（白俄罗斯）
【难度】
【出处】
1999年第40届IMO试题
【标注】
【答案】
略
【解析】
设 $n=2k$，首先将正方板黑白相间地涂成像国际象棋盘那样．设 $f(n)$ 为所求的 $N$ 的最小值，$f_w(n)$ 为必须作上标记的白格子的最小数目，使得任一黑格子都有一个作上标记的白格子与之相邻．同样地，定义 $f_b(n)$ 为必须作上标记的黑格子的最小数目，使得任一白格子都有一个作上标记的黑格子的最小数目，使得任一白格子都有一个作上标记的黑格子与之相邻．由于 $n$ 为偶数，"棋盘"是对称的．故有
$f_w(n)=f_b(n)$ ①
$f(n)=f_w(n)+f_b(n)$ ②
为方便起见，将"棋盘"按照最长的黑格子对角线水平放置，则各行黑格子点数目分别为 $2,4,\cdots,2k,\cdots,4,2$．
在含有 $4i-2$ 个黑格子的那行下面，将奇数位置的白格子作上标记，当该行在对角线上方时，共有 $2i$ 个白格子作上了标记；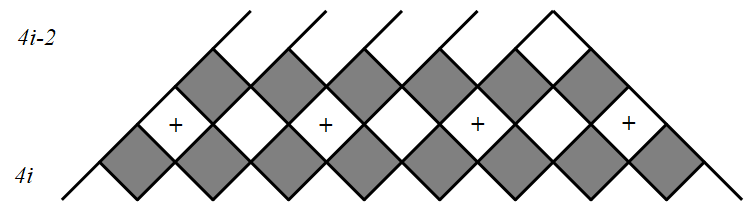
而当该行在对角线下方时，共有 $2i-1$ 个白格子作上了标记，
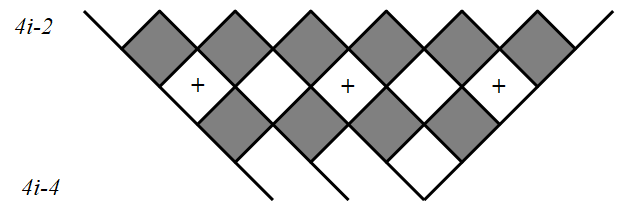因而作上标记的白格子共有
$2+4+\cdots+k+\cdots+3+1=\dfrac{k(k+1)}{2}$（个）．
易见这时每个黑格子都与一个作上标记的白格子相邻，故得
$f_w(n)\leqslant \dfrac{k(k+1)}{2}$ ③
考虑这 $\dfrac{k(k+1)}{2}$ 个作上标记的白格子，它们中的任意两个没有相邻的公共黑格子，所以，至少还需要将 $\dfrac{k(k+1)}{2}$ 个黑格子作上标记，以保证这些白格子中的每一个都有一个作上标记的黑格子与之相邻，从而
$f_b(n)\geqslant\dfrac{k(k+1)}{2}$ ④
由 ①，③，④ 得
$f_w(n)=f_b(n)=\dfrac{k(k+1)}{2}$ ⑤
由 ②⑤ 得 $f(n)=k(k+1)=\dfrac{n(n+2)}{4}$．
$f_w(n)=f_b(n)$ ①
$f(n)=f_w(n)+f_b(n)$ ②
为方便起见，将"棋盘"按照最长的黑格子对角线水平放置，则各行黑格子点数目分别为 $2,4,\cdots,2k,\cdots,4,2$．
在含有 $4i-2$ 个黑格子的那行下面，将奇数位置的白格子作上标记，当该行在对角线上方时，共有 $2i$ 个白格子作上了标记；
而当该行在对角线下方时，共有 $2i-1$ 个白格子作上了标记，因而作上标记的白格子共有$2+4+\cdots+k+\cdots+3+1=\dfrac{k(k+1)}{2}$（个）．
易见这时每个黑格子都与一个作上标记的白格子相邻，故得
$f_w(n)\leqslant \dfrac{k(k+1)}{2}$ ③
考虑这 $\dfrac{k(k+1)}{2}$ 个作上标记的白格子，它们中的任意两个没有相邻的公共黑格子，所以，至少还需要将 $\dfrac{k(k+1)}{2}$ 个黑格子作上标记，以保证这些白格子中的每一个都有一个作上标记的黑格子与之相邻，从而
$f_b(n)\geqslant\dfrac{k(k+1)}{2}$ ④
由 ①，③，④ 得
$f_w(n)=f_b(n)=\dfrac{k(k+1)}{2}$ ⑤
由 ②⑤ 得 $f(n)=k(k+1)=\dfrac{n(n+2)}{4}$．
答案
解析
备注
