1999年第40届IMO试题

• 知识点

  >

  二试几何部分

略

如图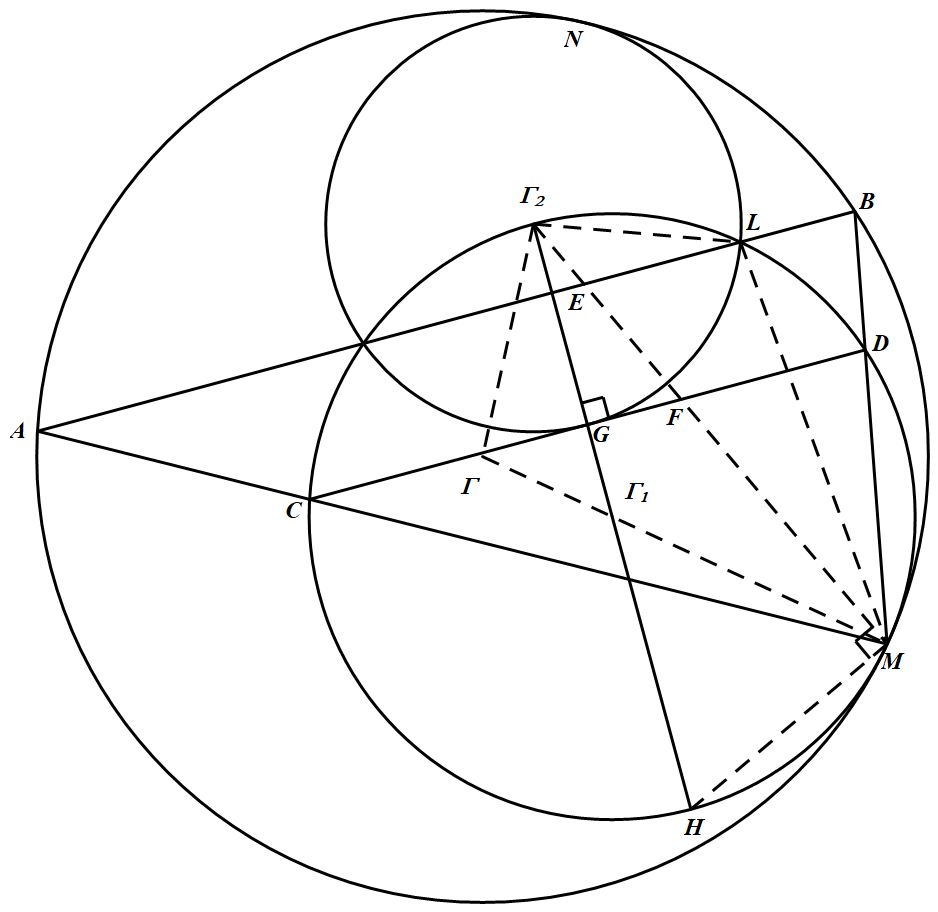设三圆圆心分别为 $\Gamma,\Gamma_1,\Gamma_2$，半径分别为 $r,r_1,r_2$．联结 $\Gamma_2\Gamma,\Gamma_1\Gamma_2,\Gamma\Gamma_1M$ 和 $\Gamma_2M$．
易知，$\Gamma\Gamma_2=r-r_2,\Gamma_1\Gamma_2=r_1,\Gamma\Gamma_1=r-r_1,\Gamma_1M=r_1$，由余弦定理 $\dfrac{F_2M^2-2r_1^2}{2r_1^2}=\cos\angle\Gamma_2\Gamma_1\Gamma=\dfrac{r_1^2+(r-r_1)^2-(r-r_2)^2}{2r_1(r-r_1)}$
解得 $\Gamma_2M^2=\dfrac{r_1r_2(2r-r_2)}{r-r_1}$．
又设 $M\Gamma_2$ 分别交 $AB,CD$ 于 $E,F$．
由于 $\odot \Gamma_1$ 和 $\odot \Gamma$ 位似中心在 $M$，故易知有 $CD\parallel AB$．
联结 $\Gamma_2\Gamma_1$，易知 $\Gamma_2\Gamma_1\perp AB$，于是 $\Gamma_2\Gamma_1\perp CD$，延长 $\Gamma_2\Gamma_1$，交 $\odot \Gamma_1$ 于 $H$，联结 $MH$．设 $\Gamma_2\Gamma_1$ 交 $CD$ 于 $G$，则 $G,H,M,F$ 共圆．于是有
$\Gamma_2G\cdot\Gamma_2H=\Gamma_2F\cdot\Gamma_2M$ ①
设 $\odot \Gamma_1$ 和 $\odot \Gamma_2$ 一交点为 $L$．由 $\angle \Gamma_2LA=\angle LM\Gamma_2$．易证 $\Gamma_2E\cdot \Gamma_2M=\Gamma_2L^2=r_2^2$．
于是 $EM=\Gamma_2M-\Gamma_2E=\Gamma_2M-\dfrac{r_2^2}{\Gamma_2M}$
而 $\dfrac{EF}{EM}=1-\dfrac{FM}{EM}=1-\dfrac{MD}{MB}=1-\dfrac{r_1}{r}$
于是 $EF=\dfrac{r-r_1}{r}\cdot\dfrac{\Gamma M^2-r_2^2}{\Gamma_2M}$．
$\Gamma_2F=\Gamma_2E+EF=\dfrac{r_2^2}{\Gamma_2M}+\dfrac{r-r_1}{r}\dfrac{\Gamma_2M^2-r_2^2}{\Gamma_2M}$
故 $\Gamma_2F\cdot \Gamma_2M=r_2^2+\dfrac{r-r_1}{r}(\Gamma_2M^2-r_2^2)=r_2^2+\dfrac{r_1r_2(2r-r_2)-(r-r_1)r_2^2}{r}=2r_1r_2$．
又 $\Gamma_2H=2r_1$，故 $\Gamma_2G=r_2$，
故 $CD$ 与 $\Gamma_2$ 相切．
证法二
过 $M,N$ 分别作切线，设交于 $P$．由于三圆根轴交于一点，$P$ 在 $AB$ 延长线上（若三根轴平行，请同学自己处理）．如图，作 $\odot \Gamma_2$ 的半径 $\Gamma_2R\perp AB$，注意 $R$ 在 $\odot \Gamma_2$ 上，目前还不知 $R$ 是否在 $CD$ 上（显然在 $CD$ 上，结论获证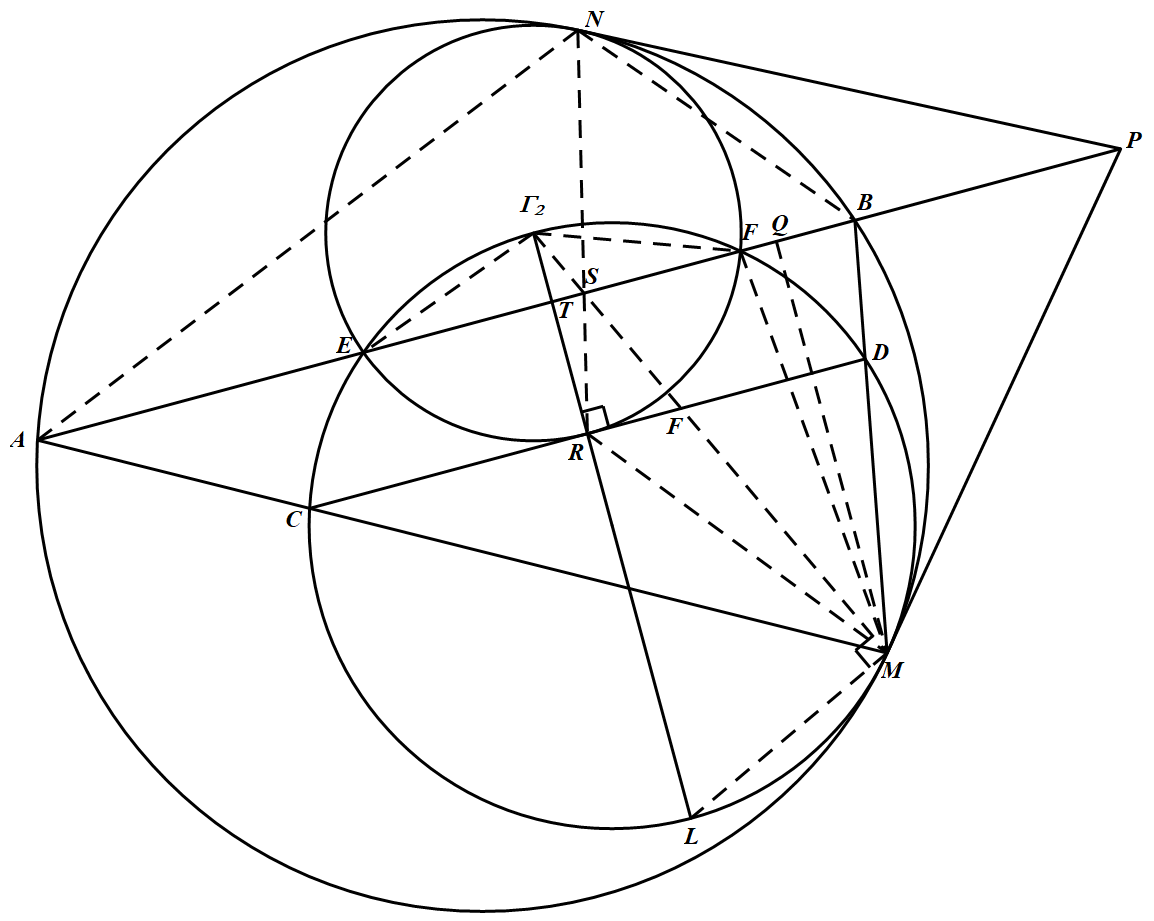）．设 $\odot \Gamma_1$ 和 $\odot \Gamma_2$ 交于 $E$ 和 $F$，$ \Gamma_2R$ 和 $EF$ 交于 $T$．
由于 $\odot \Gamma_1$ 和 $\odot \Gamma_2$ 位似，位似中心为 $M$，易知 $\dfrac{MC}{MA}=\dfrac{MD}{MB}$，故 $CD\parallel AB$．于是 $\overparen{CE}=\overparen{FD}$，而 $\overparen{\Gamma_2E}=\overparen{\Gamma_2F}$，加之，得 $\overparen{\Gamma_2C}=\overparen{\Gamma_2D}$，故 $M\Gamma_2$ 平分 $\angle AMB$，设 $M\Gamma_2$ 和 $AB$ 交于点 $S$．
同理，$NR$ 平分 $\angle ANB$，设 $NR$ 与 $AB$ 交于 $S^\prime$．
由弦切角定理及三角形相似，易知
$\dfrac{AS}{SB}=\dfrac{AM}{BM}=\dfrac{AP}{PM}=\dfrac{AP}{PN}=\dfrac{AN}{BN}=\dfrac{AS^\prime}{S^\prime B}$
于是 $S$ 与 $S^\prime$ 重合．
另外还容易得出 $PS=PM=PN$．
延长 $\Gamma_2R$ 交 $\odot \Gamma_1$ 于 $L$．联结 $\Gamma_2E,\Gamma_2F,FM$，易知
$\Gamma_2R^2=\Gamma_2S\cdot \Gamma_2M=\Gamma_2T\cdot \Gamma_2L$ ①
令 $\angle RSM=\angle RMQ=\theta,\angle\Gamma_2ST=\angle PSM=\alpha$，其中 $MQ\perp AP$，$Q$ 是垂足．
设 $\odot\Gamma,\odot\Gamma_1,\odot\Gamma_2$ 的半径分别为 $r,r_1,r_2$．于是
$\begin{aligned}
\frac{r_1}{r}&=\frac{\Gamma_2L}{2PM\tan\frac{\angle NPM}{2}}\\
&=\frac{\Gamma_2R^2}{2\Gamma_2T\cdot PM\tan\theta}\\
&=\frac{\Gamma_2S\cdot \Gamma_2M\cdot \cos\alpha}{2\Gamma_2S\sin\alpha\cdot \frac{SM}{2}\tan\theta}\\
&=\frac{TQ}{QM\tan\theta}=\frac{TQ}{QM}\cdot\frac{QM-TR}{TQ}\\
&=1-\frac{TR}{QM}=1-\frac{AC}{AM}=1-\frac{BD}{BM}
\end{aligned}$
这就证得 $R$ 在 $CD$ 上．
证法三
如图，作两小圆的一条公切线 $ST$，与 $\odot \Gamma_1,\odot \Gamma_2$ 分别切于 $F,E$．
我们回忆一系列非常熟悉的结论．
首先，不妨设 $ST$ 为 $\odot\Gamma$ 的弦，则 $NE$ 和 $MF$ 交于 $\overparen{ST}$ 的中点，不妨设为 $G$．
另一熟知结论告诉我们，$E,N,M,F$ 四点共圆，于是 $GE\cdot GN=GC\cdot GM$，$G$ 对 $\odot \Gamma_1$ 和 $\odot\Gamma_2$ 的幂相等，因此 $G$ 在 $AB$ 上，也即 $A$ 与 $G$ 重合，于是 $F$ 与 $C$ 重合．
作 $\odot \Gamma_2$ 的切线 $CL$，并延长交 $\odot \Gamma_1$ 于 $Q$．则 $\angle \Gamma_2QC=\angle \Gamma_2CS=\angle\Gamma_2CQ$，故 $\overparen{\Gamma_2C}=\overparen{\Gamma_2Q}$．
如图，设 $\odot \Gamma_1$ 和 $\odot \Gamma_2$ 交于 $K,P$ 两点，其中 $K$ 靠近 $CS$．由 $\overparen{\Gamma_2K}=\overparen{\Gamma_2P}$，得 $\overparen{KC}=\overparen{PQ}$．
于是 $CQ\parallel AB$，而 $CD\parallel AB$．于是 $D$ 与 $Q$ 重合，此即 $CD$ 与 $\odot \Gamma_2$ 相切．