在凸四边形 $ABCD$ 中，两对角线 $AC$ 与 $BD$ 互相垂直，两对边 $AB$ 和 $DC$ 不平行．点 $P$ 为 线段 $AB$ 及 $CD$ 的垂直平分线的交点，且 $P$ 在四边形 $ABCD$ 内部．求证：$ABCD$ 为圆内接四边形的充分条件是 $\triangle ABP$ 与 $\triangle CDP$ 的面积相等．（卢森堡）
【难度】
【出处】
1998年第39届IMO试题
【标注】
【答案】
略
【解析】
如图，不妨设 $BA$ 和 $CD$ 延长后交于 $Q$，$AC$ 与 $BD$ 交于 $G,E,F$ 分别为 $AB$ 与 $CD$ 的中点，$EG$ 延长后交 $CD$ 于 $H$．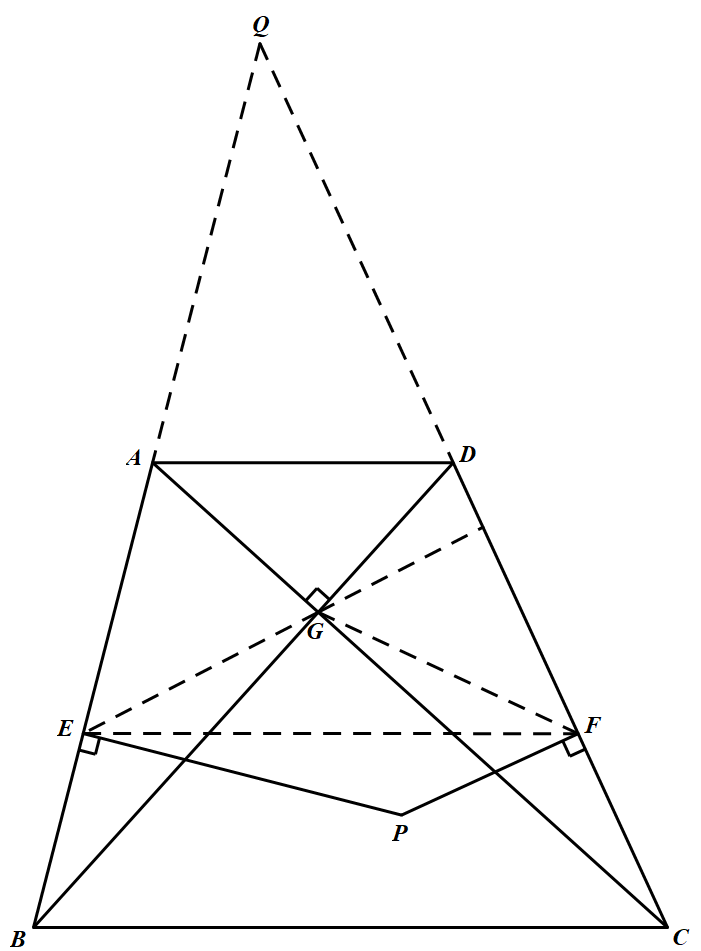
若 $A,B,C,D$ 共圆，由 $AE=EG$ 和 $AG\perp BG$ 得 $\angle HGC=\angle AGE=\angle GAE=\angle BDC$．
由此易知 $EH\perp CD$，所以 $EG\parallel PF$．同理可证 $GF\parallel PE$．于是四边形 $PFGE$ 为平行四边形．
于是
$\begin{aligned}
S_{\triangle ABP}&=\dfrac{1}{2}AB\cdot PE\\
&=\frac{1}{2}AB\cdot GF=\frac{1}{4}AB\cdot CD\\
&=\frac{1}{2}PF\cdot CD=S_{\triangle CDP}
\end{aligned}$
必要性得证．
另一方面，若 $S_{\triangle ABP}=S_{\triangle CDP}$，则有 $\dfrac{EG}{GF}=\dfrac{AB}{CD}=\dfrac{PF}{EP}$．
又
$\begin{aligned}
\angle P&=180^\circ-\angle Q\\
&=180^\circ-(90^\circ-\angle ABD-\angle ACD)\\
&=90^\circ+\angle EGB+\angle FGC\\
&=\angle EGF
\end{aligned}$
从而 $\triangle GEF\sim\triangle PFE$，又 $EF=EF$，故有 $\triangle GEF\cong\triangle PFE$．于是四边形 $PFGE$ 为平行四边形．于是 $GE\perp CD$，这表明
$\begin{aligned}
\angle CDB&=90^\circ-\angle DGH\\
&=90^\circ-\angle EGB=90^\circ-\angle ABG\\
&=\angle BAC
\end{aligned}$
所以 $A,B,C,D$ 四点共圆．充分性获证．
若 $A,B,C,D$ 共圆，由 $AE=EG$ 和 $AG\perp BG$ 得 $\angle HGC=\angle AGE=\angle GAE=\angle BDC$．由此易知 $EH\perp CD$，所以 $EG\parallel PF$．同理可证 $GF\parallel PE$．于是四边形 $PFGE$ 为平行四边形．
于是
$\begin{aligned}
S_{\triangle ABP}&=\dfrac{1}{2}AB\cdot PE\\
&=\frac{1}{2}AB\cdot GF=\frac{1}{4}AB\cdot CD\\
&=\frac{1}{2}PF\cdot CD=S_{\triangle CDP}
\end{aligned}$
必要性得证．
另一方面，若 $S_{\triangle ABP}=S_{\triangle CDP}$，则有 $\dfrac{EG}{GF}=\dfrac{AB}{CD}=\dfrac{PF}{EP}$．
又
$\begin{aligned}
\angle P&=180^\circ-\angle Q\\
&=180^\circ-(90^\circ-\angle ABD-\angle ACD)\\
&=90^\circ+\angle EGB+\angle FGC\\
&=\angle EGF
\end{aligned}$
从而 $\triangle GEF\sim\triangle PFE$，又 $EF=EF$，故有 $\triangle GEF\cong\triangle PFE$．于是四边形 $PFGE$ 为平行四边形．于是 $GE\perp CD$，这表明
$\begin{aligned}
\angle CDB&=90^\circ-\angle DGH\\
&=90^\circ-\angle EGB=90^\circ-\angle ABG\\
&=\angle BAC
\end{aligned}$
所以 $A,B,C,D$ 四点共圆．充分性获证．
答案
解析
备注
