设 $I$ 是 $\triangle ABC$ 的内心，并设 $\triangle ABC$ 的内切圆与三边 $BC,CA,AB$ 分别相切于 $K,L,M$，过点 $B$ 平行于 $MK$ 的直线分别交直线 $LM$ 及 $LK$ 于 点 $R$ 和 $S$．求证：$\angle RIS$ 是锐角．（乌克兰）
【难度】
【出处】
1998年第39届IMO试题
【标注】
【答案】
略
【解析】
如图，联结 $MI,BI$．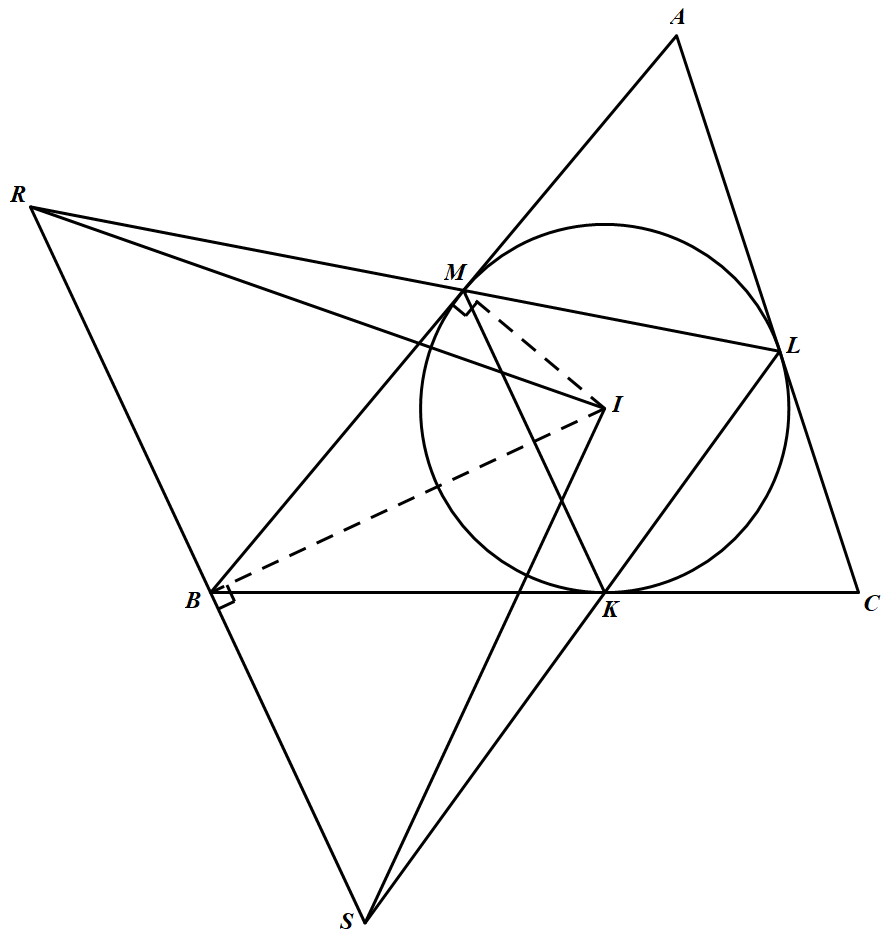
又 $BI\perp MK$ 而 $RS\parallel MK$，故 $BI\perp RS$．
又由 $RS\parallel MK$ 知 $\angle BSK=\angle MKL$；$\angle KBS=\angle MKB=\angle MLK$．
于是 $\triangle KBS\sim\triangle MLK$．从而 $\dfrac{BS}{BK}=\dfrac{LK}{LM}$．
同理可证，$\dfrac{BR}{BM}=\dfrac{LM}{LK}$．
可知 $BR\cdot RS=BM\cdot BK=BM^2<BI^2$．
又由 $BI\perp RS$，知在 $BI$ 内存在点 $P$，使得 $BR\cdot BS=BP^2$，在 $\triangle RPS$ 中，根据射影定理或相似形，可知 $\angle RPS=90^\circ$，于是点 $I$ 在以 $RS$ 为直径的圆外，从而 $\angle RIS<90^\circ$．
又 $BI\perp MK$ 而 $RS\parallel MK$，故 $BI\perp RS$．又由 $RS\parallel MK$ 知 $\angle BSK=\angle MKL$；$\angle KBS=\angle MKB=\angle MLK$．
于是 $\triangle KBS\sim\triangle MLK$．从而 $\dfrac{BS}{BK}=\dfrac{LK}{LM}$．
同理可证，$\dfrac{BR}{BM}=\dfrac{LM}{LK}$．
可知 $BR\cdot RS=BM\cdot BK=BM^2<BI^2$．
又由 $BI\perp RS$，知在 $BI$ 内存在点 $P$，使得 $BR\cdot BS=BP^2$，在 $\triangle RPS$ 中，根据射影定理或相似形，可知 $\angle RPS=90^\circ$，于是点 $I$ 在以 $RS$ 为直径的圆外，从而 $\angle RIS<90^\circ$．
答案
解析
备注
