查看数据源：5c86171e210b28428f14d569
在坐标平面上，具有整数坐标的点构成单位边长的正方格的顶点．这些正方格被涂上黑白相间的两种颜色（像国际象棋棋盘那样）．
对于任意一对正整数 $m$ 和 $n$，考虑一个直角三角形，它的顶点具有整数坐标，两条直角边的长度分别为 $m$ 和 $n$，且两条直角边都在这些正方格的边上．
令 ${S}_{1}$ 为这个三角形区域中所有黑色部分的总面积，${S}_{2}$ 则 为所有白色部分的总面积．令 $f(m,n)=|{S}_{1}-{S}_{2}|$．
（1）当 $m$ 和 $n$ 同为正偶数或同为正奇数时，计算 $f(m,n)$ 的值；
（2）求证：$f(m,n)\leqslant \frac{1}{2}\max \{m,n\}$ 对于所有的 $m$ 和 $n$ 都成立；
（3）求证：不存在常数 $c$，使得对所有 $m$ 和 $n$，不等式 $f(m,n)<c$ 都成立．（白俄罗斯）
【难度】
【出处】
1997年第38届IMO试题
【标注】
  • 知识点
    >
    二试组合部分
【答案】
略
【解析】
（1）设 $\triangle ABC$ 为一直角三角形，它的顶点具有整数坐标，且两条直角边都在这些正方格的边上．设 $\angle A=90^\circ,AB=m,AC=n$．考虑如下图中的矩形 $ABCD$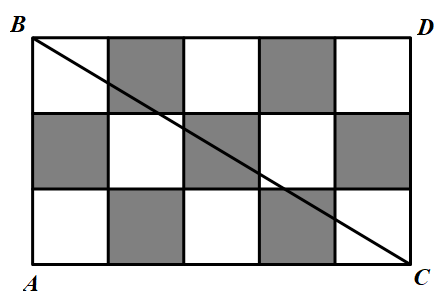．对于任一多边形 $P$，记 $S_1(P)$ 为 $P$ 中黑色部分的面积，$S_2(P)$ 为 $P$ 中白色部分的面积．
当 $m$ 和 $n$ 同时为偶数或者同时为奇数时，矩形 $ABCD$ 的着色关于斜边 $BC$ 的中点中心对称．因此
$f(m,n)=|S_1(ABC)-S_2(ABC)|=\dfrac{1}{2}\left|S_1(ABCD)-S_2(ABCD)\right|$
于是，当 $m$ 和 $n$ 同时为偶数时，$f(m,n)=0$，而当 $m$ 和 $n$ 同时为奇数时，$f(m,n)=\dfrac{1}{2}$．
（2）如果 $m$ 和 $n$ 同时为偶数或者同时为奇数，那么由（1）即知结论成立．故可设 $m$ 为奇数，$n$ 为偶数．如图所示，考虑 $AB$ 上的点 $L$，使得 $AL=m-1$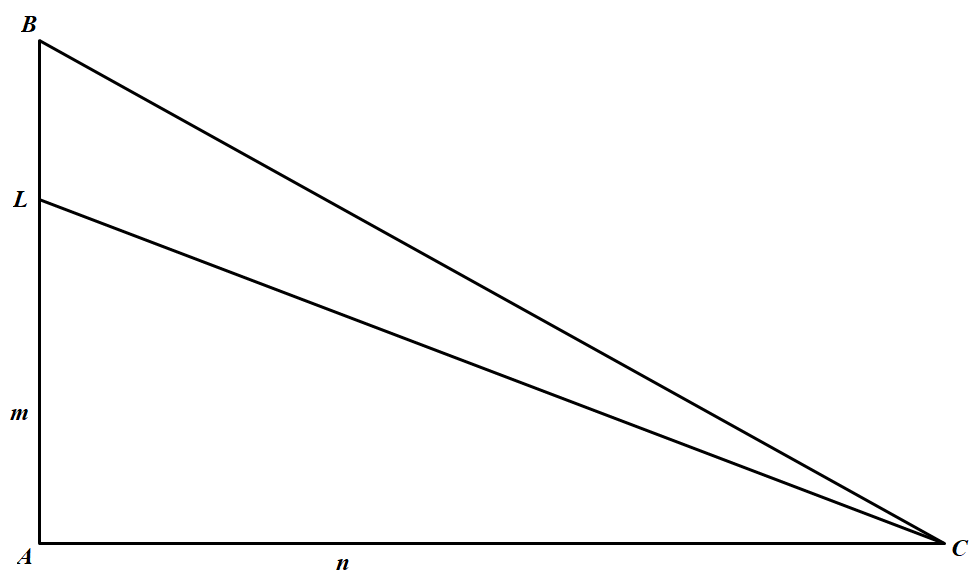．由于 $m-1$ 为偶数，我们有 $f(m-1,n)=0$，即 $S_1(ALC)=S_2(ALC)$．因此
$\begin{aligned}
f(m,n)&=|S_1(ABC)-S_2(ABC)|\\
&=|S_1(LBC)-S_2(LBC)|\\
&\leqslant \triangle LBC的面积=\frac{n}{2}\leqslant \frac{1}{2}\max\{m,n\}
\end{aligned}$
（3）我们来计算 $f(2k+1,2k)$ 的值．在下图中，考虑 $AB$ 上的点 $L$，使得 $AL=2k$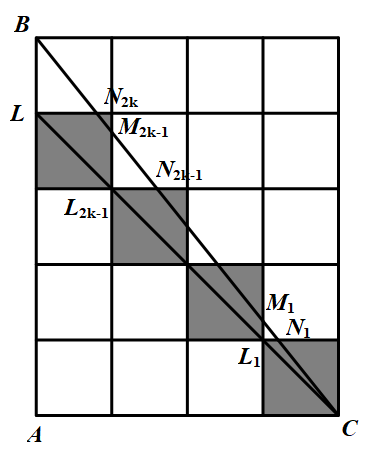．因为 $f(2k,2k)=0$，且 $S_1(ALC)=S_2(ALC)$．我们有 $f(2k+1,2k)=|S_1(LBC)-S_2(LBC)|$，$\triangle LBC$ 的面积等于 $k$．不妨假设对角线 $LC$ 全部落在黑色方格中．于是，$LBC$ 的白色部分由若干个三角形组成：$BLN_{2k},M_{2k-1}L_{2k-1}N_{2k-1},\cdots,M_1L_1N_1$，它们每一个都与 $\triangle BAC$ 相似．其总面积等于
$\begin{aligned}
S_2(LBC)&=\frac{1}{2}\cdot \frac{2k}{2k+1}\left(\left(\dfrac{2k}{2k}\right)^2+\left(\dfrac{2k-1}{2k}\right)^2+\cdots+\left(\dfrac{1}{2k}\right)^2\right)\\
&=\frac{1}{4k(2k+1)}(1^2+2^2+\cdots+(2k)^2)\\
&=\frac{4k+1}{12}
\end{aligned}$
因此，黑色部分的总面积为
$S_1(LBC)=k-\dfrac{1}{12}(4k+1)=\dfrac{1}{12}(8k-1)$
$f(2k+1,2k)=\dfrac{2k-1}{6}$
可以取任意大的值．
答案 解析 备注
0.115733s