设 $\angle A$ 是 $\triangle ABC$ 中最小的角．点 $B$ 和 $C$ 将这个三角形的外接圆分成两段弧．设 $U$ 是落在不含 $A$ 的那段弧上且不等于 $B$ 与 $C$ 的一个点．线段 $AB$ 和 $AC$ 的垂直平分线分别交线段 $AU$ 于 $V$ 和 $W$．直线 $BV$ 和 $CW$ 相 交于 $T$．求证：$AU=TB+TC$．（英国）
【难度】
【出处】
1997年第38届IMO试题
【标注】
【答案】
略
【解析】
由 $\angle A$ 的性质知 $\angle WCA=\angle WAC<\angle A\leqslant \angle C$，故延长 $CW$ 交外接圆 $\overparen{AB}$ 上一点，记为 $S$．如图，联结 $BS,BU$．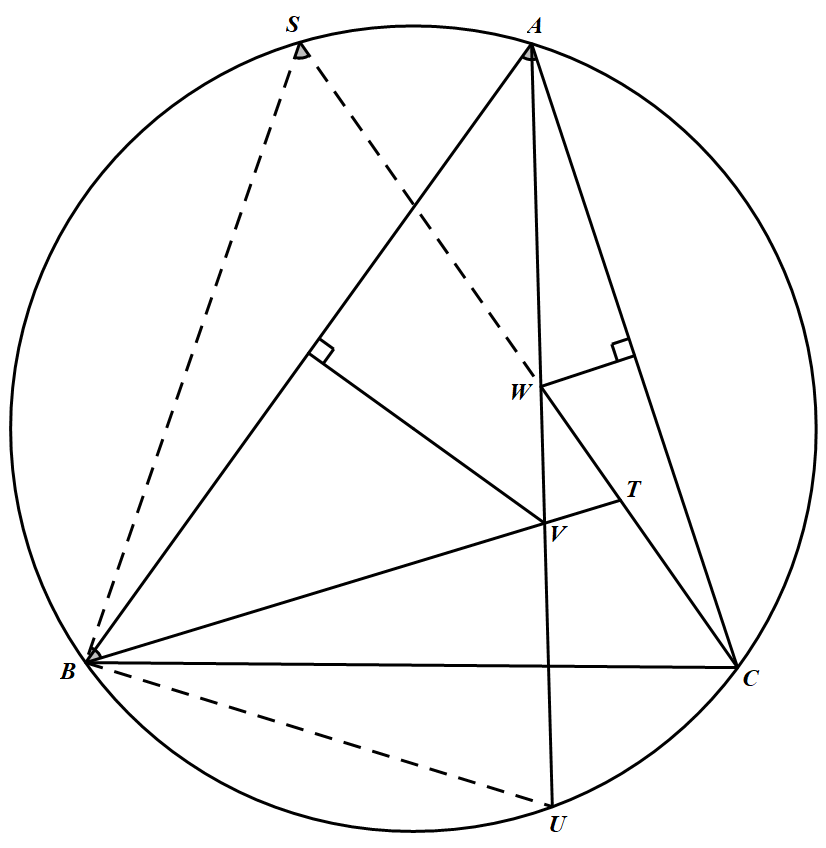
易知 $AV=BV,AW=CW$．
于是
$\begin{aligned}
\angle S&=\angle A=\angle BAU+\angle CAU\\
&=\angle VBA+\angle SCA\\
&=\angle VBA+\angle SBA\\
&=\angle SBV
\end{aligned}$
因此 $ST=BT,TB+TC=SC$．
由此可知，剩下只要证明 $AU=SC$ 即可．设外接圆半径为 $R$．
于是
$\begin{aligned}
AU&=2R\sin\angle ABU\\
&=2R\sin(\angle B+\angle CBU)\\
&=2R\sin(\angle B+\angle CAU)\\
&=2R\sin(\angle B+\angle ACS)\\
&=2R\sin(\angle B+\angle ABS)\\
&=2R\sin\angle SBC\\
&=SC
\end{aligned}$
证毕．
易知 $AV=BV,AW=CW$．于是
$\begin{aligned}
\angle S&=\angle A=\angle BAU+\angle CAU\\
&=\angle VBA+\angle SCA\\
&=\angle VBA+\angle SBA\\
&=\angle SBV
\end{aligned}$
因此 $ST=BT,TB+TC=SC$．
由此可知，剩下只要证明 $AU=SC$ 即可．设外接圆半径为 $R$．
于是
$\begin{aligned}
AU&=2R\sin\angle ABU\\
&=2R\sin(\angle B+\angle CBU)\\
&=2R\sin(\angle B+\angle CAU)\\
&=2R\sin(\angle B+\angle ACS)\\
&=2R\sin(\angle B+\angle ABS)\\
&=2R\sin\angle SBC\\
&=SC
\end{aligned}$
证毕．
答案
解析
备注
