设 $P$ 是 $\triangle ABC$ 内一点，$\angle APB-\angle ACB=\angle APC-\angle ABC$．又设 $D、E$ 分别是 $\triangle APB$ 及 $\triangle APC$ 的内心，求证：$AP、BD、CE$ 交于一点．（加拿大）
【难度】
【出处】
1996年第37届IMO试题
【标注】
【答案】
略
【解析】
由角平分线性质定理知，显然只要证明 $\dfrac{AB}{BP}=\dfrac{AC}{CP}$ 即可．
下面就来证明此式．
如图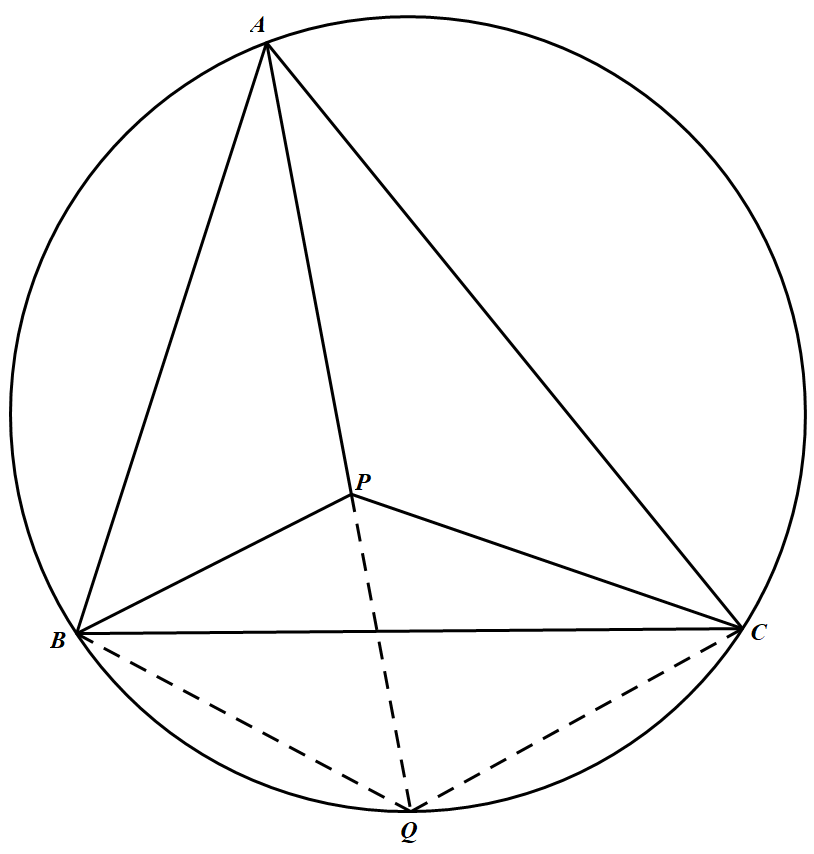
作 $\triangle ABC$ 外接圆，延长 $AP$ 交圆于 $Q$，联结 $BQ,CQ$，由四点共圆及条件知，有
$\begin{aligned}
\angle PBQ&=\angle APB-\angle AQB\\
&=\angle APB-\angle ACB\\
&=\angle APC-\angle ABC\\
&=\angle APC-\angle AQC\\
&=\angle PCQ
\end{aligned}$
于是，由正弦定理知
$\begin{aligned}
\frac{BP}{CP}&=\frac{PQ\cdot \frac{\sin\angle PQB}{\sin\angle PBQ}}{PQ\cdot\frac{\sin\angle PQC}{\sin\angle PCQ}}\\
&=\frac{\sin\angle PQB}{\sin\angle PQC}=\frac{\sin\angle ACB}{\sin\angle ABC}\\
&=\frac{AB}{AC}
\end{aligned}$
下面就来证明此式．
如图
作 $\triangle ABC$ 外接圆，延长 $AP$ 交圆于 $Q$，联结 $BQ,CQ$，由四点共圆及条件知，有$\begin{aligned}
\angle PBQ&=\angle APB-\angle AQB\\
&=\angle APB-\angle ACB\\
&=\angle APC-\angle ABC\\
&=\angle APC-\angle AQC\\
&=\angle PCQ
\end{aligned}$
于是，由正弦定理知
$\begin{aligned}
\frac{BP}{CP}&=\frac{PQ\cdot \frac{\sin\angle PQB}{\sin\angle PBQ}}{PQ\cdot\frac{\sin\angle PQC}{\sin\angle PCQ}}\\
&=\frac{\sin\angle PQB}{\sin\angle PQC}=\frac{\sin\angle ACB}{\sin\angle ABC}\\
&=\frac{AB}{AC}
\end{aligned}$
答案
解析
备注
