设 $A、B、C、D$ 是一条直线上依次排列的四个不同的点，分别以 $AC,BD$ 为直径的圆相交于 $X$ 和 $Y$，直线 $XY$ 交 $BC$ 于 $Z$．若 $P$ 为直线 $XY$ 上异于 $Z$ 的一点，直线 $CP$ 与以 $AC$ 为直径的圆交于 $C$ 及 $M$，直线 $BP$ 与以 $BD$ 为直径的圆相交于 $B$ 及 $N$，试证：$AM、DN、XY$ 三线共点．（保加利亚）
【难度】
【出处】
1995年第36届IMO试题
【标注】
【答案】
略
【解析】
如图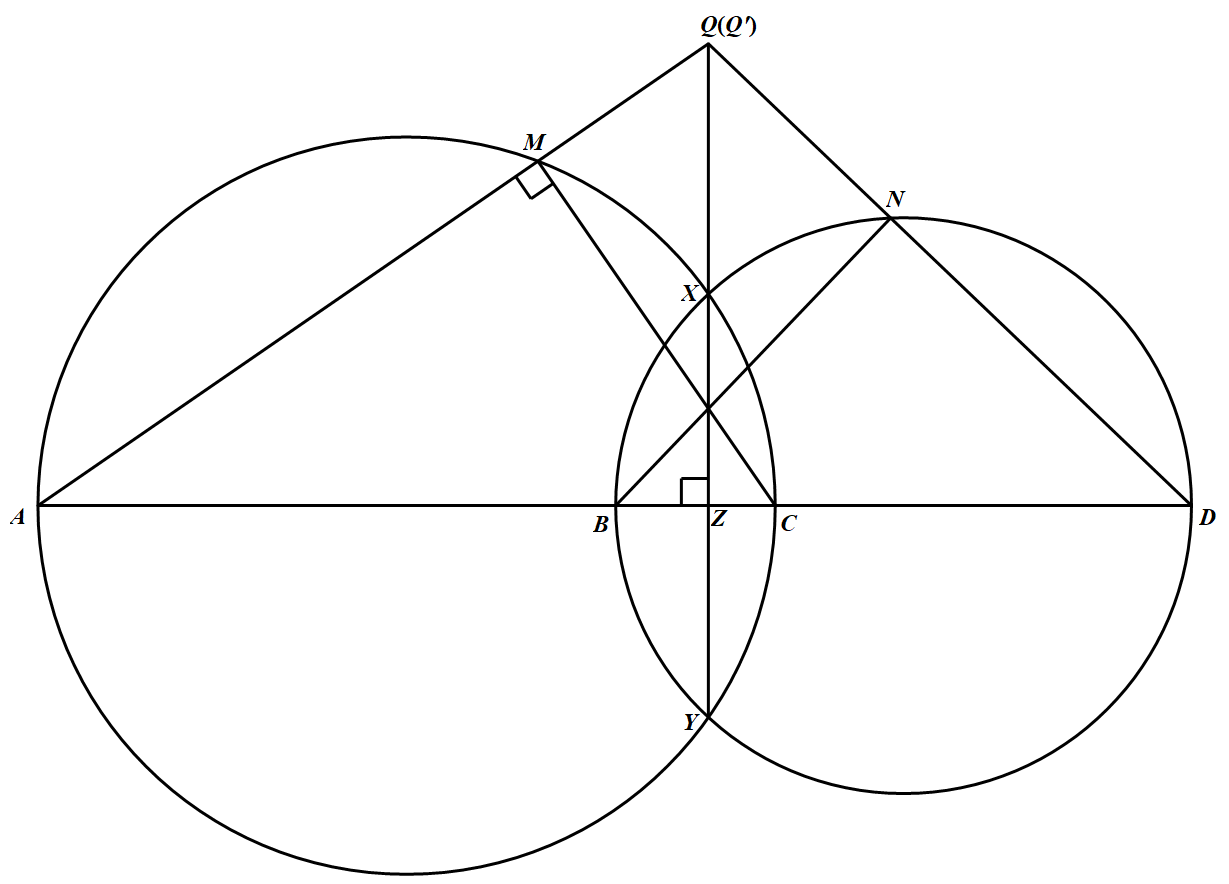
设 $AM$ 直线，$DN$ 直线与 $XY$ 直线分别交于 $Q$ 和 $Q^\prime$．
易知 $\angle AMC=90^\circ$，因此 $\triangle QAZ\sim\triangle CPZ$，于是 $QZ=\dfrac{CZ\cdot AZ}{PZ}=\dfrac{XZ\cdot YZ}{PZ}$．
同理 $Q^\prime Z=\dfrac{BZ\cdot DZ}{PZ}=\dfrac{XZ\cdot YZ}{PZ}$．
因而 $QZ=Q^\prime Z$，$Q$ 与 $Q^\prime$ 重合，此即 $AM,DN$ 和 $XY$ 三线共点．
设 $AM$ 直线，$DN$ 直线与 $XY$ 直线分别交于 $Q$ 和 $Q^\prime$．易知 $\angle AMC=90^\circ$，因此 $\triangle QAZ\sim\triangle CPZ$，于是 $QZ=\dfrac{CZ\cdot AZ}{PZ}=\dfrac{XZ\cdot YZ}{PZ}$．
同理 $Q^\prime Z=\dfrac{BZ\cdot DZ}{PZ}=\dfrac{XZ\cdot YZ}{PZ}$．
因而 $QZ=Q^\prime Z$，$Q$ 与 $Q^\prime$ 重合，此即 $AM,DN$ 和 $XY$ 三线共点．
答案
解析
备注
