设凸六边形 $ABCDEF$，满足 $AB=BC=CD,DE=EF=FA,\angle BCD=\angle EFA=60^\circ$．设 $G$ 和 $H$ 是这六边形内部的两点，使得 $\angle AGB=\angle DHE=120^\circ$．试证：$AG+GB+GH+DH+HE\geqslant CF$．（新西兰）
【难度】
【出处】
1995年第36届IMO试题
【标注】
【答案】
略
【解析】
如图，联结 $BD,AE$．易见四边形 $ABDE$ 为一筝形．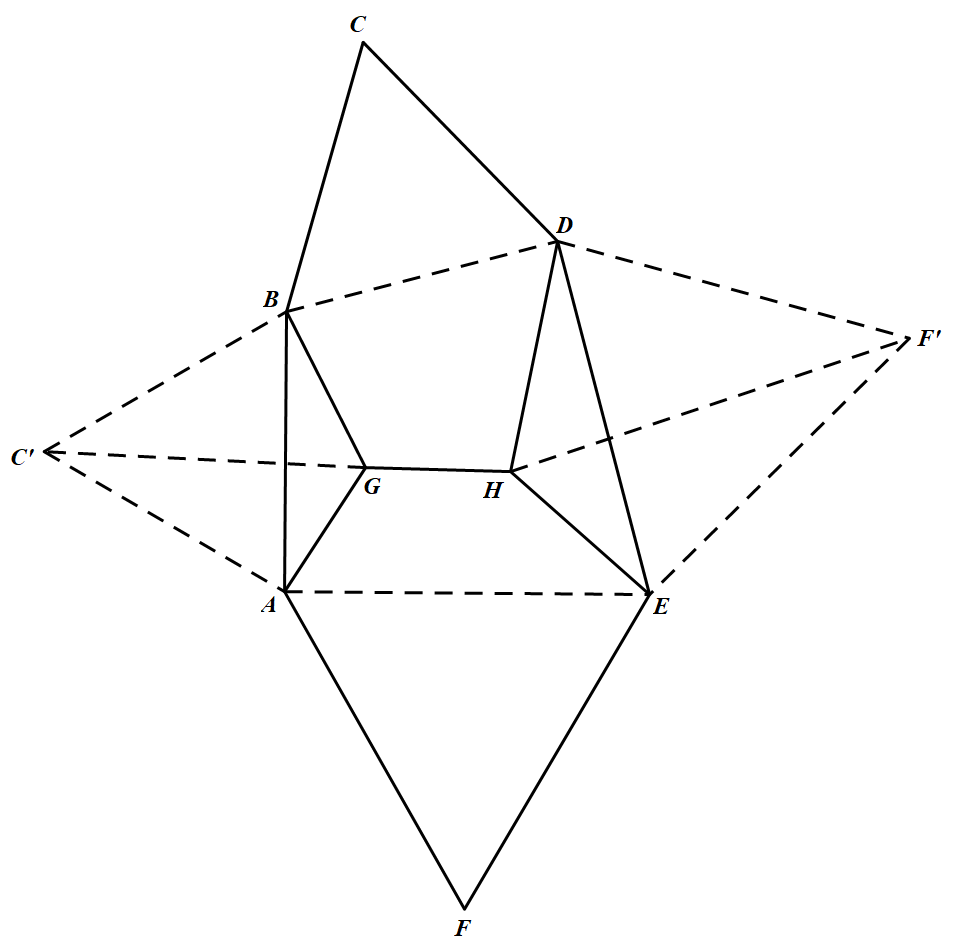
向外作正三角形 $ABC^\prime$ 与 $DF^\prime E$，联结 $C^\prime G,F^\prime H$．
易见 $C^\prime$ 与 $C$ 关于 $BE$ 对称，$F$ 与 $F^\prime $ 也是这样，于是 $CF=C^\prime F^\prime $．
由托勒密定理知 $C^\prime G=AG+GB,HF^\prime =DH+HE$．
于是
$\begin{aligned}
&AG+GB+GH+DH+HE\\
&=C^\prime G+GH+HF^\prime\\
&\geqslant C^\prime F^\prime\\
&=CF
\end{aligned}$
向外作正三角形 $ABC^\prime$ 与 $DF^\prime E$，联结 $C^\prime G,F^\prime H$．易见 $C^\prime$ 与 $C$ 关于 $BE$ 对称，$F$ 与 $F^\prime $ 也是这样，于是 $CF=C^\prime F^\prime $．
由托勒密定理知 $C^\prime G=AG+GB,HF^\prime =DH+HE$．
于是
$\begin{aligned}
&AG+GB+GH+DH+HE\\
&=C^\prime G+GH+HF^\prime\\
&\geqslant C^\prime F^\prime\\
&=CF
\end{aligned}$
答案
解析
备注
