设 $D$ 是锐角三角形 $ABC$ 内部的一点，使 $\angle ADB=\angle ACB+90^\circ$，并有 $AC·BD$ = $AD·BC$
（$a$）计算比值 $\dfrac{AB\cdot CD}{AC\cdot BD}$；
（$b$）求证：$\triangle ACD$ 的外接圆和 $\triangle BCD$ 的外接圆在 $C$ 点的切线互相垂直．（英国）
（$a$）计算比值 $\dfrac{AB\cdot CD}{AC\cdot BD}$；
（$b$）求证：$\triangle ACD$ 的外接圆和 $\triangle BCD$ 的外接圆在 $C$ 点的切线互相垂直．（英国）
【难度】
【出处】
1993年第34届IMO试题
【标注】
【答案】
略
【解析】
（$a$）作 $\triangle CEB\sim\triangle CDA$，如图，其中 $\angle CAD=\angle CBE,\angle ACD=\angle BCE$．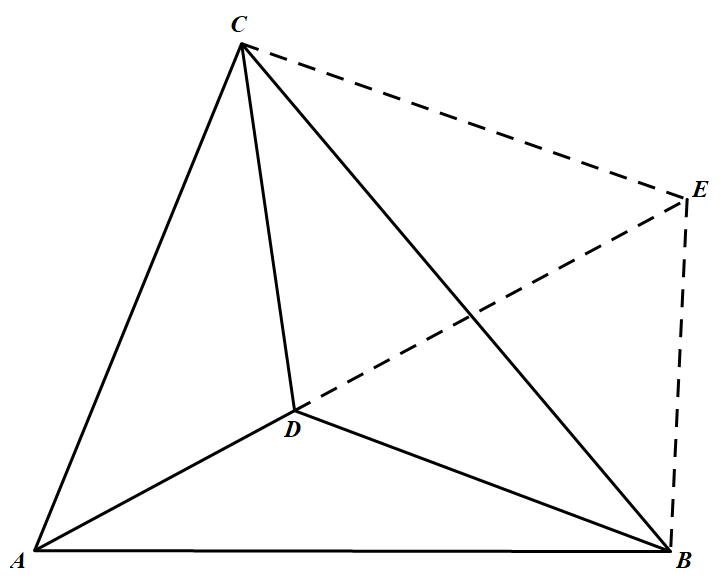
由条件及相似，知 $\dfrac{BE}{BC}=\dfrac{AD}{AC}=\dfrac{BD}{BC}$．
因此 $BE=BD$．又
$\begin{aligned}\angle ADB&=\angle CAD+\angle CBD+\angle ACB\\
&=\angle DBE+\angle ACB\\
&=90^\circ+\angle ACB
\end{aligned}$
于是 $\angle DBE=90^circ$，$\triangle BDE$ 为等腰直角三角形．
又易知 $\angle ACB=\angle DCE,\dfrac{AC}{CD}=\dfrac{BC}{CE}$，故有 $\triangle ACB\sim\triangle DCE$．
于是 $\dfrac{AB\cdot CD}{AC\cdot BD}=\dfrac{DE}{BD}=\sqrt{2}$．
（$b$）假定 $\triangle ACD,\triangle BCD$ 外接圆在 $C$ 点的切线分别是 $CF$ 和 $CG$（图中未画出），使弦切角 $\angle FCD=\angle DBC,\angle GCD=\angle CAD$．
于是
$\begin{aligned}
\angle FCG&=\angle FCD+\angle GCD\\
&=\angle DBC+\angle CAD\\
&=\angle ADB-\angle ACB\\
&=90^\circ
\end{aligned}$
即两线垂直．
由条件及相似，知 $\dfrac{BE}{BC}=\dfrac{AD}{AC}=\dfrac{BD}{BC}$．因此 $BE=BD$．又
$\begin{aligned}\angle ADB&=\angle CAD+\angle CBD+\angle ACB\\
&=\angle DBE+\angle ACB\\
&=90^\circ+\angle ACB
\end{aligned}$
于是 $\angle DBE=90^circ$，$\triangle BDE$ 为等腰直角三角形．
又易知 $\angle ACB=\angle DCE,\dfrac{AC}{CD}=\dfrac{BC}{CE}$，故有 $\triangle ACB\sim\triangle DCE$．
于是 $\dfrac{AB\cdot CD}{AC\cdot BD}=\dfrac{DE}{BD}=\sqrt{2}$．
（$b$）假定 $\triangle ACD,\triangle BCD$ 外接圆在 $C$ 点的切线分别是 $CF$ 和 $CG$（图中未画出），使弦切角 $\angle FCD=\angle DBC,\angle GCD=\angle CAD$．
于是
$\begin{aligned}
\angle FCG&=\angle FCD+\angle GCD\\
&=\angle DBC+\angle CAD\\
&=\angle ADB-\angle ACB\\
&=90^\circ
\end{aligned}$
即两线垂直．
答案
解析
备注
