在一个可以无限扩展的方格棋盘上，一个游戏按下述规则进行：
首先，把 ${n}^{2}$ 枚棋子放在由相连的小方格组成的 $n×n$ 的方块中，每个小方格里放一枚棋子，这个游戏的每一个允许的步骤是：把一枚棋子沿水平方向或者垂直方向跨越相邻并放有棋子的一个小方格进入下一个小方格，如果那里是空着的；否则不允许，然后即把被跨越的那枚棋子拿掉．
求 $n$ 的所有这样的值，对每一个这样的值存在一种玩法，使得这游戏最终导致棋盘上只剩下一枚棋子．（芬兰）
首先，把 ${n}^{2}$ 枚棋子放在由相连的小方格组成的 $n×n$ 的方块中，每个小方格里放一枚棋子，这个游戏的每一个允许的步骤是：把一枚棋子沿水平方向或者垂直方向跨越相邻并放有棋子的一个小方格进入下一个小方格，如果那里是空着的；否则不允许，然后即把被跨越的那枚棋子拿掉．
求 $n$ 的所有这样的值，对每一个这样的值存在一种玩法，使得这游戏最终导致棋盘上只剩下一枚棋子．（芬兰）
【难度】
【出处】
1993年第34届IMO试题
【标注】
【答案】
略
【解析】
首先证明：若 $3|n$，则不存在玩法，使最终只剩下一枚棋子．
把无限的方格棋盘中的方格分成三类，如图所示：
$\begin{array}{c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|}\hline
\cdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\cdots\\\hline
\cdots&A&B&C&A&B&C&A&B&C&A&B&C&A&\cdots\\\hline
\cdots&B&C&A&B&C&A&B&C&A&B&C&A&B&\cdots\\\hline
\cdots&C&A&B&C&A&B&C&A&B&C&A&B&C&\cdots\\\hline
\cdots&A&B&C&A&B&C&A&B&C&A&B&C&A&\cdots\\\hline
\cdots&B&C&A&B&C&A&B&C&A&B&C&A&B&\cdots\\\hline
\cdots&C&A&B&C&A&B&C&A&B&C&A&B&C&\cdots\\\hline
\cdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\cdots\\\hline
\end{array}$
易见对任意一个 $3\times 3$ 的小方块，都有 $3$ 个 $A$，$3$ 个 $B$，$3$ 个 $C$．$i$ 步后 $A,B,C$ 三类方格中的棋子分别记为 $S_A^i,S_B^i,S_C^i$，则当 $3|n$ 时，$S_A^0=S_B^0=S_C^0=\dfrac{n^2}{3}$
所以 $S_A^0,S_B^0,S_C^0$ 的奇偶性相同．每一步使两个类各少一枚棋子，另一类增加一枚棋子，所以 $S_A^i,S_B^i,S_C^i$ 的奇偶性仍然相同，永远不会出现两个为 $0$，一个为 $1$ 的情况．
因此，当 $3|n$ 时，不存在最终只剩一枚棋子的玩法．
下面证明当 $3\nmid n$ 时，即 $n=3k+1$ 或 $3k+2$ 时，一定存在玩法，使最终只剩下一枚棋子．
首先对如图的" $L$ "形四个方格都存在棋子时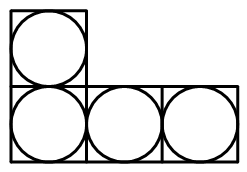
，可以采用如下玩法：
去掉排在一排的 $3$ 枚棋子，并使剩下的一枚在原来位置．
现在用数学归纳法来证明上面的论断（下图）．
当 $k=0$ 时，$n=1$，显然成立．对 $n=2$ 有如下玩法；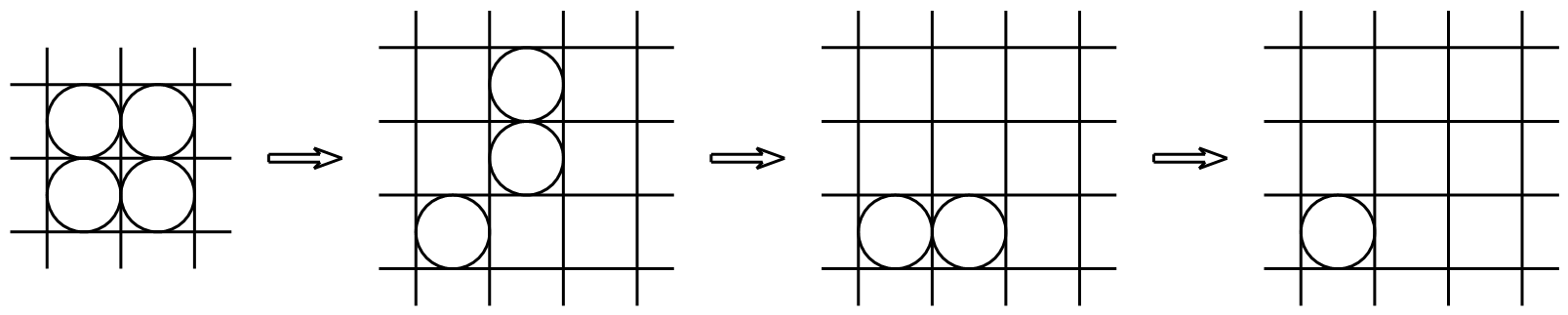
假设对于 $k$，所说玩法存在．对于 $k+1$，将初始的 $n\times n$ 方阵分成四块：
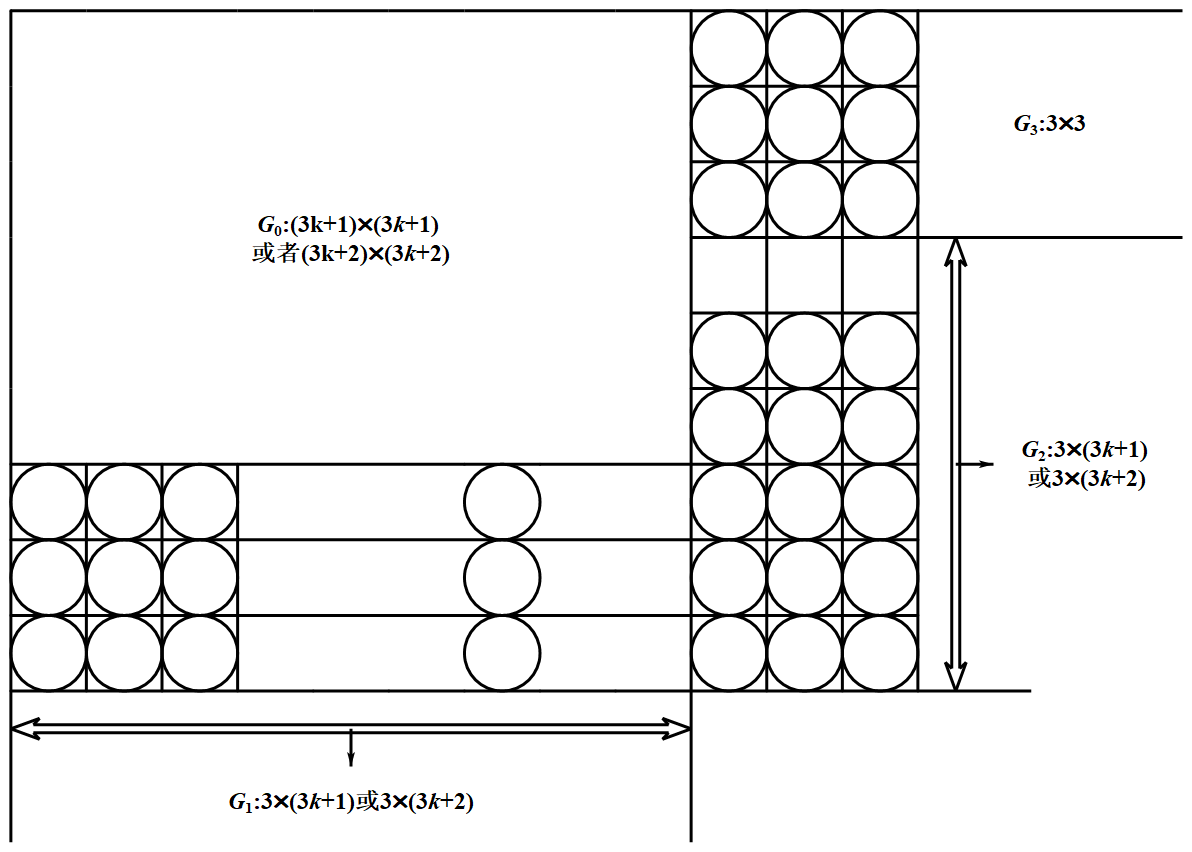采用开始所说的玩法可以由左向右地将 $G_1$ 中每一竖列的棋子 $3$ 个 $3$ 个地拿掉，而其余的棋子不动，然后由上而下地把 $G_2$ 中每一横行的棋子 $3$ 个 $3$ 个地拿掉，其余的棋子不动，最后，从右向左地把 $G_3$ 中每一竖列的棋子 $3$ 个 $3$ 个地拿掉．
根据归纳假设，$G_0$ 中的棋子存在玩法，使最终只剩下一个棋子．
于是，对于 $3\nmid n$，存在玩法，使最终只剩下一枚棋子．
把无限的方格棋盘中的方格分成三类，如图所示：
$\begin{array}{c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|}\hline
\cdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\cdots\\\hline
\cdots&A&B&C&A&B&C&A&B&C&A&B&C&A&\cdots\\\hline
\cdots&B&C&A&B&C&A&B&C&A&B&C&A&B&\cdots\\\hline
\cdots&C&A&B&C&A&B&C&A&B&C&A&B&C&\cdots\\\hline
\cdots&A&B&C&A&B&C&A&B&C&A&B&C&A&\cdots\\\hline
\cdots&B&C&A&B&C&A&B&C&A&B&C&A&B&\cdots\\\hline
\cdots&C&A&B&C&A&B&C&A&B&C&A&B&C&\cdots\\\hline
\cdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\cdots\\\hline
\end{array}$
易见对任意一个 $3\times 3$ 的小方块，都有 $3$ 个 $A$，$3$ 个 $B$，$3$ 个 $C$．$i$ 步后 $A,B,C$ 三类方格中的棋子分别记为 $S_A^i,S_B^i,S_C^i$，则当 $3|n$ 时，$S_A^0=S_B^0=S_C^0=\dfrac{n^2}{3}$
所以 $S_A^0,S_B^0,S_C^0$ 的奇偶性相同．每一步使两个类各少一枚棋子，另一类增加一枚棋子，所以 $S_A^i,S_B^i,S_C^i$ 的奇偶性仍然相同，永远不会出现两个为 $0$，一个为 $1$ 的情况．
因此，当 $3|n$ 时，不存在最终只剩一枚棋子的玩法．
下面证明当 $3\nmid n$ 时，即 $n=3k+1$ 或 $3k+2$ 时，一定存在玩法，使最终只剩下一枚棋子．
首先对如图的" $L$ "形四个方格都存在棋子时
，可以采用如下玩法：去掉排在一排的 $3$ 枚棋子，并使剩下的一枚在原来位置．现在用数学归纳法来证明上面的论断（下图）．
当 $k=0$ 时，$n=1$，显然成立．对 $n=2$ 有如下玩法；
假设对于 $k$，所说玩法存在．对于 $k+1$，将初始的 $n\times n$ 方阵分成四块：采用开始所说的玩法可以由左向右地将 $G_1$ 中每一竖列的棋子 $3$ 个 $3$ 个地拿掉，而其余的棋子不动，然后由上而下地把 $G_2$ 中每一横行的棋子 $3$ 个 $3$ 个地拿掉，其余的棋子不动，最后，从右向左地把 $G_3$ 中每一竖列的棋子 $3$ 个 $3$ 个地拿掉．根据归纳假设，$G_0$ 中的棋子存在玩法，使最终只剩下一个棋子．
于是，对于 $3\nmid n$，存在玩法，使最终只剩下一枚棋子．
答案
解析
备注
