给定空间中的 $9$ 个点，其中任何 $4$ 点都不共面，在每一对点之间都连有一条线段，这条线段可染为红色或蓝色，也可不染色．试求出最小的 $n$ 值，使得将其中任意 $n$ 条线段中的每一条任意地染为红蓝二色之一时，在这 $n$ 条线段的集合中都必包含有一个各边同色的三角形．（中国）
【难度】
【出处】
1992年第33届IMO试题
【标注】
【答案】
略
【解析】
设染色的线段至少有 $33$ 条，则不染色的线段至少有 $\mathrm{C}_9^2-33=36-33=3$（条）．
若点 $A_1$ 引出不染色的线段，去掉 $A_1$ 及 $A_1$ 所引出的线段，如果剩下的图中，还有点 $A_2$ 引出不染色的线段，去掉 $A_2$ 及 $A_2$ 所引出的线段，依次进行下去，由于不染色的线段至多 $3$ 条，所以至多去掉 $3$ 个顶点（以及从它们所引出的线段），剩下的至少 $6$ 个点，每两点之间的联线染上了红色或蓝色．易知其中必有一个同色三角形．
下面的例子说明：若染色的线段数小于 $33$ 时，未必有同色三角形．如图所示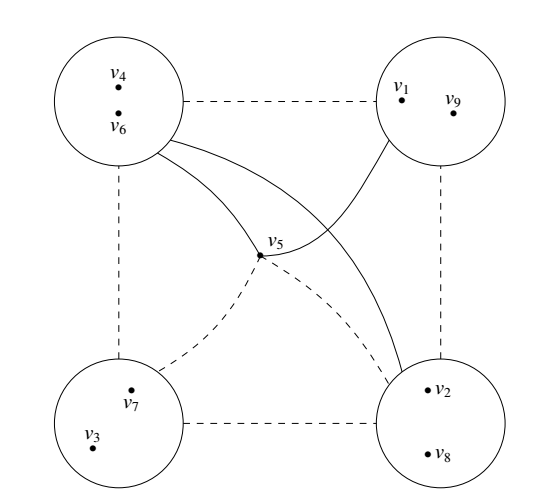
$v_1$ 与 $v_9$，$v_2$ 与 $v_8$，$v_3$ 与 $v_7$，$v_4$ 与 $v_6$ 之间的边不染色，且图中的实线表示红色，虚线表示蓝色，$v_1,v_9$ 与 $v_2,v_8$ 之间的虚线表示 $v_1v_2,v_1,v_8,v_9,v_2,v_9,v_8$ 均为虚线，其余类似．则图中没有同色三角形．
若点 $A_1$ 引出不染色的线段，去掉 $A_1$ 及 $A_1$ 所引出的线段，如果剩下的图中，还有点 $A_2$ 引出不染色的线段，去掉 $A_2$ 及 $A_2$ 所引出的线段，依次进行下去，由于不染色的线段至多 $3$ 条，所以至多去掉 $3$ 个顶点（以及从它们所引出的线段），剩下的至少 $6$ 个点，每两点之间的联线染上了红色或蓝色．易知其中必有一个同色三角形．
下面的例子说明：若染色的线段数小于 $33$ 时，未必有同色三角形．如图所示
$v_1$ 与 $v_9$，$v_2$ 与 $v_8$，$v_3$ 与 $v_7$，$v_4$ 与 $v_6$ 之间的边不染色，且图中的实线表示红色，虚线表示蓝色，$v_1,v_9$ 与 $v_2,v_8$ 之间的虚线表示 $v_1v_2,v_1,v_8,v_9,v_2,v_9,v_8$ 均为虚线，其余类似．则图中没有同色三角形．
答案
解析
备注
