在一个平面中，$C$ 为一个圆周，直线 $L$ 是圆周的一条 的切线，$M$ 为 $L$ 上一点，试求出具有如下性质的所有点 $P$ 的集合：在 直线 $L$ 上存在两点 $Q$ 和 $R$，使得 $M$ 是线段 $QR$ 的中点，且 $C$ 是 $\triangle PQR$ 的内切圆．（法国）
【难度】
【出处】
1992年第33届IMO试题
【标注】
【答案】
略
【解析】
如图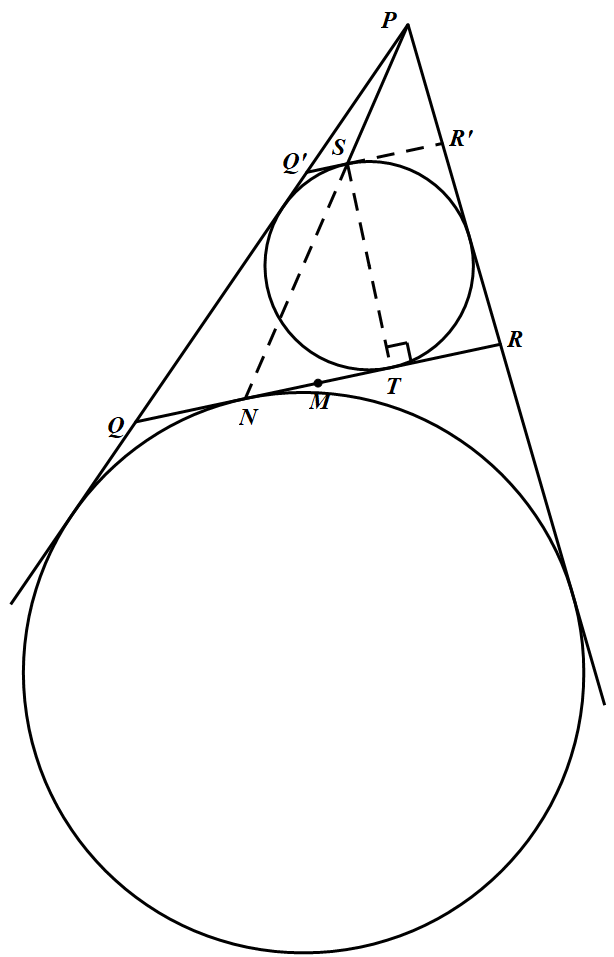
设 $\odot C$ 与 $L$ 切于 $T$，$TS$ 为 $\odot C$ 的一条直径．
过 $S$ 作直线平行于 $QR$，分别交 $PR$ 于 $R^\prime $，交 $PQ$ 于 $Q^\prime$．
易知 $P$ 为 $\triangle PQ^\prime R^\prime$ 与 $\triangle PQR$ 之位似中心，$\odot C$ 成立 $\triangle PQ^\prime R^\prime$ 的旁切圆．$PS$ 直线与 $QR$ 的交点即为 $\triangle PQR$ 的（$\angle P$ 内）旁切圆在 $QR$ 上的切点．
易知 $QN=TR=\dfrac{1}{2}(PR+RQ-QP)$．
这样 $M$ 仍为 $NT$ 中点．
于是，可作 $N$，使 $MN=MT$，联结 $NS$ 并延长，$P$ 便在这条延长的射线上（不含 $S$）．
反之，在上述射线上任找一点 $P$，作 $\odot C$ 的切线，它们必与 $MN$ 直线相交，不妨设交点分别为 $Q,R$，易证 $M$ 为 $QR$ 中点．
综上所述，所求轨迹为 $NS$ 的延长线（以 $S$ 为端点的射线，但不含 $S$）．
设 $\odot C$ 与 $L$ 切于 $T$，$TS$ 为 $\odot C$ 的一条直径．过 $S$ 作直线平行于 $QR$，分别交 $PR$ 于 $R^\prime $，交 $PQ$ 于 $Q^\prime$．
易知 $P$ 为 $\triangle PQ^\prime R^\prime$ 与 $\triangle PQR$ 之位似中心，$\odot C$ 成立 $\triangle PQ^\prime R^\prime$ 的旁切圆．$PS$ 直线与 $QR$ 的交点即为 $\triangle PQR$ 的（$\angle P$ 内）旁切圆在 $QR$ 上的切点．
易知 $QN=TR=\dfrac{1}{2}(PR+RQ-QP)$．
这样 $M$ 仍为 $NT$ 中点．
于是，可作 $N$，使 $MN=MT$，联结 $NS$ 并延长，$P$ 便在这条延长的射线上（不含 $S$）．
反之，在上述射线上任找一点 $P$，作 $\odot C$ 的切线，它们必与 $MN$ 直线相交，不妨设交点分别为 $Q,R$，易证 $M$ 为 $QR$ 中点．
综上所述，所求轨迹为 $NS$ 的延长线（以 $S$ 为端点的射线，但不含 $S$）．
答案
解析
备注
