设圆内两弦 $AB,CD$ 交于圆内一点 $E$，在直线段 $EB$ 的内部取一点 $M$，然后过点 $D、E、M$ 作圆，再过 $E$ 作此圆的切线分别交直线 $BC,AC$ 于点 $F,G$．若已知 $\dfrac{AM}{AB}=t$，试用 $t$ 表示 $\dfrac{EG}{EF}$．（印度）
【难度】
【出处】
1990年第31届IMO试题
【标注】
【答案】
略
【解析】
如图所示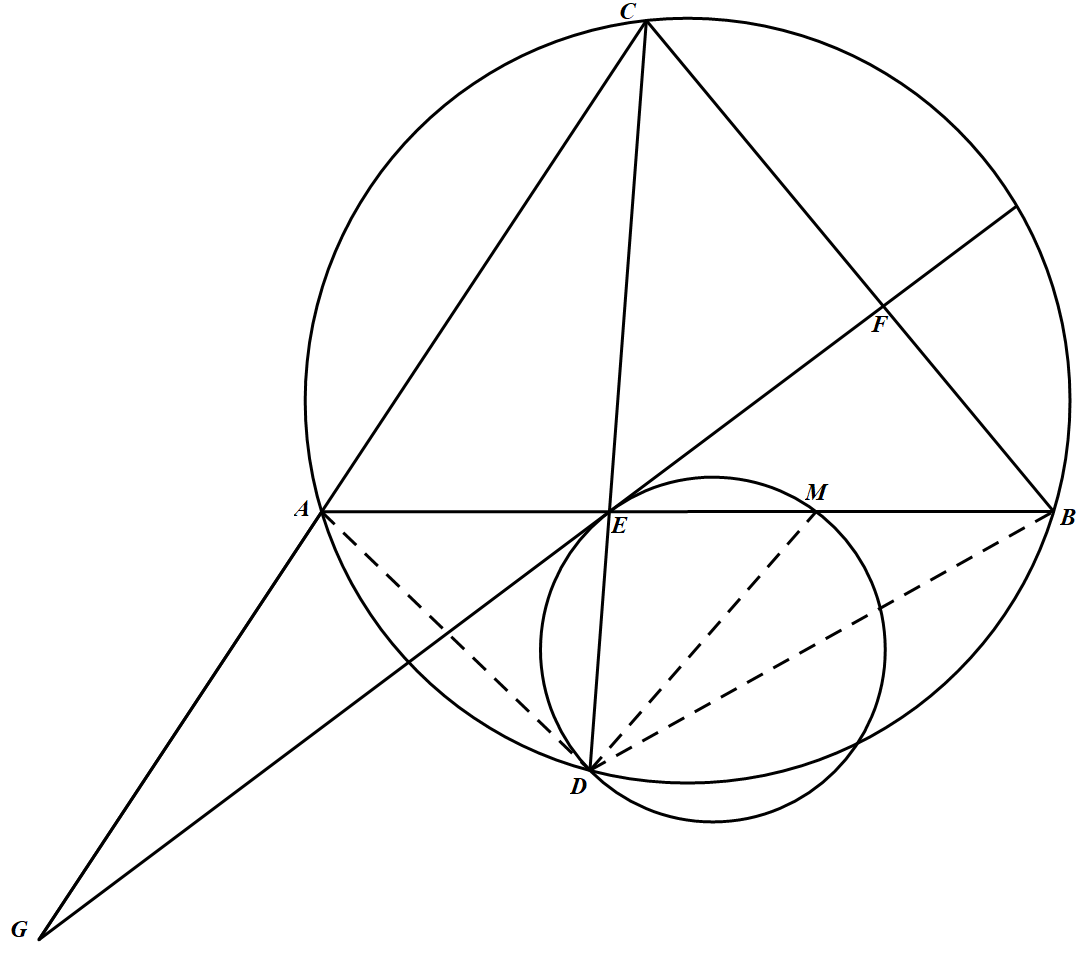
联结 $AD,MD$ 及 $BD$．
易知有
$\angle CEF=\angle DEG=\angle EMD$
$\angle ECF=\angle MAD$
于是 $\triangle CEF\sim\triangle ADM$
故 $CE\cdot MD=AM\cdot EF$．
另外，又有
$\begin{aligned}
\angle ECG&=\angle MBD\\
\angle CEG&=\angle 180^\circ-\angle GED\\
&=180^\circ-\angle EMD\\
&=\angle BMD
\end{aligned}$
因此 $\triangle CGE\sim\triangle BDM$，从而 $GE\cdot MB=CE\cdot MD$．
这样一来，便有 $GE\cdot MB=AM\cdot EF$，故
$\dfrac{EG}{EF}=\dfrac{AM}{MB}=\dfrac{t\cdot AB}{(1-t)\cdot AB}=\dfrac{t}{1-t}$．
联结 $AD,MD$ 及 $BD$．易知有
$\angle CEF=\angle DEG=\angle EMD$
$\angle ECF=\angle MAD$
于是 $\triangle CEF\sim\triangle ADM$
故 $CE\cdot MD=AM\cdot EF$．
另外，又有
$\begin{aligned}
\angle ECG&=\angle MBD\\
\angle CEG&=\angle 180^\circ-\angle GED\\
&=180^\circ-\angle EMD\\
&=\angle BMD
\end{aligned}$
因此 $\triangle CGE\sim\triangle BDM$，从而 $GE\cdot MB=CE\cdot MD$．
这样一来，便有 $GE\cdot MB=AM\cdot EF$，故
$\dfrac{EG}{EF}=\dfrac{AM}{MB}=\dfrac{t\cdot AB}{(1-t)\cdot AB}=\dfrac{t}{1-t}$．
答案
解析
备注
