已知 $\triangle ABC$ 是锐角三角形，$\angle A,\angle B,\angle C$ 的平分线延长后分别与 $\triangle ABC$ 的外接圆交于 ${A}_{1},{B}_{1},{C}_{1}$，直线 $A{A}_{1}$ 与 $\angle B,\angle C$ 的外角平分线交于 ${A}_{0}$，类似地得到点 ${B}_{0}$ 和 ${C}_{0}$．求证：
（1）$\triangle {A}_{0}{B}_{0}{C}_{0}$ 的面积是六边形 $A{C}_{1}B{A}_{1}C{B}_{1}$ 面积的两倍；
（2）$\triangle {A}_{0}{B}_{0}{C}_{0}$ 的面积至少是 $\triangle ABC$ 面积的四倍．（澳大利亚）
（1）$\triangle {A}_{0}{B}_{0}{C}_{0}$ 的面积是六边形 $A{C}_{1}B{A}_{1}C{B}_{1}$ 面积的两倍；
（2）$\triangle {A}_{0}{B}_{0}{C}_{0}$ 的面积至少是 $\triangle ABC$ 面积的四倍．（澳大利亚）
【难度】
【出处】
1989年第30届IMO试题
【标注】
【答案】
略
【解析】
（1）如图，易知 $\angle A_1IC=\dfrac{1}{2}(\angle A+\angle C)=\angle A_1CI$．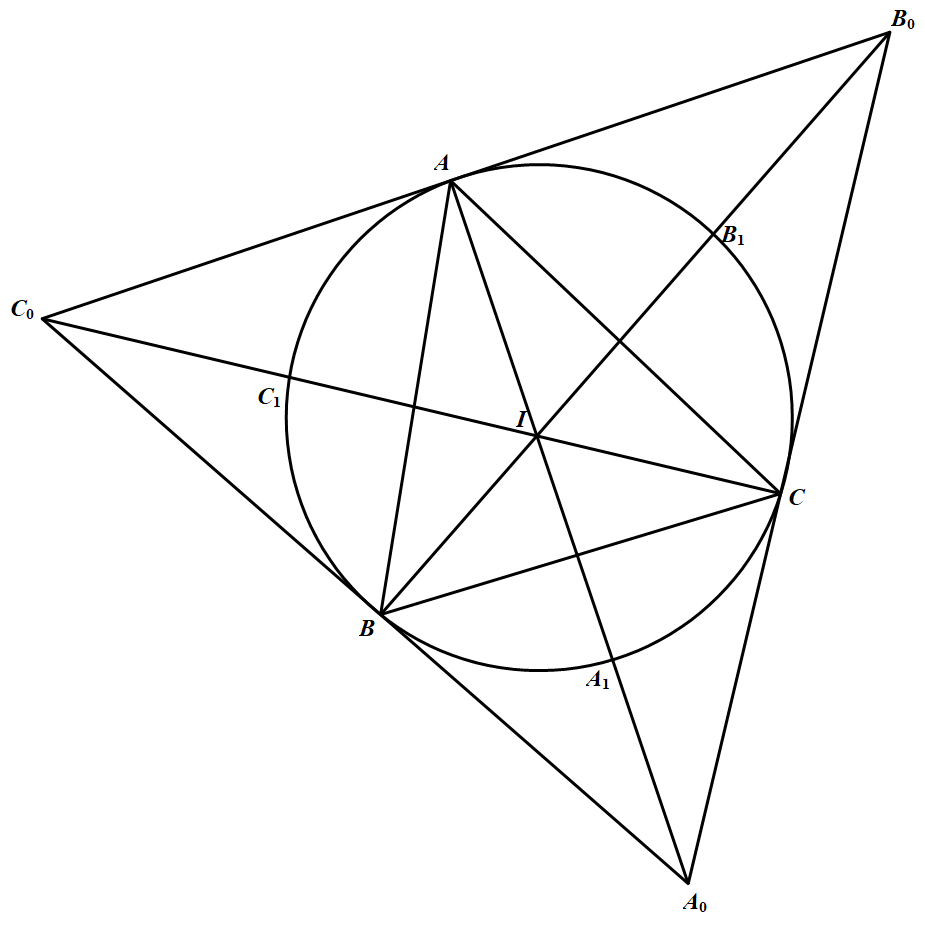
因此有 $IA-1=CA_1$．
这里 $I$ 是 $\triangle ABC$ 之内心．
又 $\angle ICA_0=90^\circ$．
因此 $A_1$ 为 $A_0I$ 之中点，故 $S_{四边形IBA_0C}=2S_{四边形IBA_1C}$；
同理 $S_{四边形AIBC_0}=2S_{四边形AIBC_1}$；$S_{四边形AICB_0}=2S_{四边形AICB_1}$．
将上述三式相加，即得 $S_{\triangle A_0B_0C_0}=2S_{六边形AC_1BA_1CB_1}$．
（2）显然只须证明 $S_{六边形AC_1BA_1CB_1}\geqslant 2S_{\triangle ABC}$ 即可．
找到 $\triangle ABC$ 之外心 $O$，易知 $OA_1\perp BC$，设 $\triangle ABC$ 三边分别为 $a,b,c$，外接圆半径为 $R$，则 $S_{四边形OBA_1C}=\dfrac{1}{2}Ra$，同理
$S_{四边形OAC_1B}=\dfrac{1}{2}Rc$
$S_{四边形AOCB_1}=\dfrac{1}{2}Rb$
因此 $S_{六边形AC_1BA_1CB_1}=\dfrac{1}{2}R(a+b+c)$．
问题就归结为证明 $R(a+b+c)\geqslant 4S_{\triangle ABC}$．
由正弦定理及面积公式，知上式等价于证明
$\sin A+\sin B+\sin C\geqslant 4\sin A\sin B\sin C$．
基本不等式告诉我们左式 $\geqslant 3\sqrt[3]{\sin A\sin B\sin C}$．若能证明 $3\sqrt[3]{\sin A\sin B\sin C}\geqslant 4\sin A\sin B\sin C$ 则大功告成，而这个不等式等价于 $\sin A\sin B\sin C\leqslant\dfrac{3\sqrt{3}}{8}$．
此不等式很常见，可用积化和差处理之，注意等号成立，仅当 $\angle A=\angle B=\angle C=60^\circ$．
因此有 $IA-1=CA_1$．这里 $I$ 是 $\triangle ABC$ 之内心．
又 $\angle ICA_0=90^\circ$．
因此 $A_1$ 为 $A_0I$ 之中点，故 $S_{四边形IBA_0C}=2S_{四边形IBA_1C}$；
同理 $S_{四边形AIBC_0}=2S_{四边形AIBC_1}$；$S_{四边形AICB_0}=2S_{四边形AICB_1}$．
将上述三式相加，即得 $S_{\triangle A_0B_0C_0}=2S_{六边形AC_1BA_1CB_1}$．
（2）显然只须证明 $S_{六边形AC_1BA_1CB_1}\geqslant 2S_{\triangle ABC}$ 即可．
找到 $\triangle ABC$ 之外心 $O$，易知 $OA_1\perp BC$，设 $\triangle ABC$ 三边分别为 $a,b,c$，外接圆半径为 $R$，则 $S_{四边形OBA_1C}=\dfrac{1}{2}Ra$，同理
$S_{四边形OAC_1B}=\dfrac{1}{2}Rc$
$S_{四边形AOCB_1}=\dfrac{1}{2}Rb$
因此 $S_{六边形AC_1BA_1CB_1}=\dfrac{1}{2}R(a+b+c)$．
问题就归结为证明 $R(a+b+c)\geqslant 4S_{\triangle ABC}$．
由正弦定理及面积公式，知上式等价于证明
$\sin A+\sin B+\sin C\geqslant 4\sin A\sin B\sin C$．
基本不等式告诉我们左式 $\geqslant 3\sqrt[3]{\sin A\sin B\sin C}$．若能证明 $3\sqrt[3]{\sin A\sin B\sin C}\geqslant 4\sin A\sin B\sin C$ 则大功告成，而这个不等式等价于 $\sin A\sin B\sin C\leqslant\dfrac{3\sqrt{3}}{8}$．
此不等式很常见，可用积化和差处理之，注意等号成立，仅当 $\angle A=\angle B=\angle C=60^\circ$．
答案
解析
备注
