考虑在同一平面上，半径分别为 $R$ 与 $r(R>r)$ 的两个同心圆．设 $P$ 是小圆周上一个交点，$B$ 是大圆周上的一个动点，直线 $BP$ 与大圆周的另一交点为 $C$，通过点 $P$ 且与 $BP$ 垂直的直线 $l$ 与小圆的另一交点为 $A$（如果 $l$ 与小圆切于 $P$，则 $A=P$）．试求：
（1）表达式 ${AB}^{2}+{BC}^{2}+{CA}^{2}$ 所取值的集合；
（2）线段 $AB$ 中点的轨迹．（卢森堡）
（1）表达式 ${AB}^{2}+{BC}^{2}+{CA}^{2}$ 所取值的集合；
（2）线段 $AB$ 中点的轨迹．（卢森堡）
【难度】
【出处】
1988年第29届IMO试题
【标注】
【答案】
略
【解析】
（1）设两圆圆心为 $O$．过 $O$ 作 $OQ\perp BC$，则易知
$BP=\dfrac{BC}{2}+PQ,CP=\dfrac{BC}{2}-PQ$（不妨设 $BP\geqslant CP$）．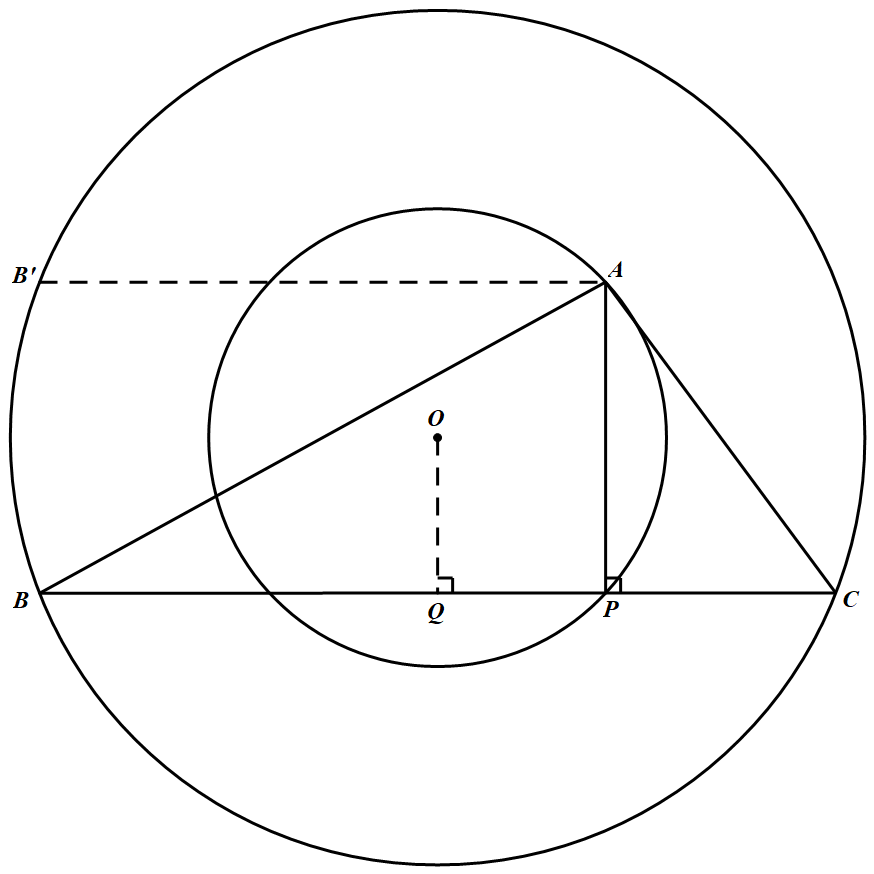
于是由勾股定理及 $AP=2OQ$，有
$\begin{aligned}
AB^2+BC^2+CA^2&=BP^2+CP^2+2AP^2+BC^2\\
&=\frac{3}{2}BC^2+2AP^2+2PQ^2\\
&=\frac{3}{2}(BC^2+AP^2)+\frac{1}{2}AP^2+2PQ^2\\
&=6(BQ^2+OQ^2)+2(PQ^2+OQ^2)\\
&=6R^2+2r^2
\end{aligned}$
这是一个常数，与 $B$ 的位置无关．
（2）作矩形 $BPAB^\prime$．易知 $B^\prime$ 在大圆周上，如图所示．
因此，$AB$ 中点即 $B^\prime P$ 中点，当 $B$ 在大圆周上变动一周时，$B^\prime$ 也在大圆周上变动一周．易知，轨迹为以 $OP$ 中点为圆心，以 $\dfrac{R}{2}$ 为半径的一个圆周．
$BP=\dfrac{BC}{2}+PQ,CP=\dfrac{BC}{2}-PQ$（不妨设 $BP\geqslant CP$）．
于是由勾股定理及 $AP=2OQ$，有$\begin{aligned}
AB^2+BC^2+CA^2&=BP^2+CP^2+2AP^2+BC^2\\
&=\frac{3}{2}BC^2+2AP^2+2PQ^2\\
&=\frac{3}{2}(BC^2+AP^2)+\frac{1}{2}AP^2+2PQ^2\\
&=6(BQ^2+OQ^2)+2(PQ^2+OQ^2)\\
&=6R^2+2r^2
\end{aligned}$
这是一个常数，与 $B$ 的位置无关．
（2）作矩形 $BPAB^\prime$．易知 $B^\prime$ 在大圆周上，如图所示．
因此，$AB$ 中点即 $B^\prime P$ 中点，当 $B$ 在大圆周上变动一周时，$B^\prime$ 也在大圆周上变动一周．易知，轨迹为以 $OP$ 中点为圆心，以 $\dfrac{R}{2}$ 为半径的一个圆周．
答案
解析
备注
