在直角三角形 $ABC$ 中，$AD$ 是 斜边 $BC$ 上的高，过 $\triangle ABD$ 的内心与 $\triangle ACD$ 的内心的直线分别交边 $AB$ 和 $AC$ 于 $K$ 和 $L$，$\triangle ABC$ 和 $\triangle AKL$ 的面积 分别记为 $S$ 和 $T$．求证：$S\geqslant2T$．（希腊）
【难度】
【出处】
1988年第29届IMO试题
【标注】
【答案】
略
【解析】
如图，设 $\triangle ABC$ 与 $\triangle ACD$ 的内心分别为 $M,N$．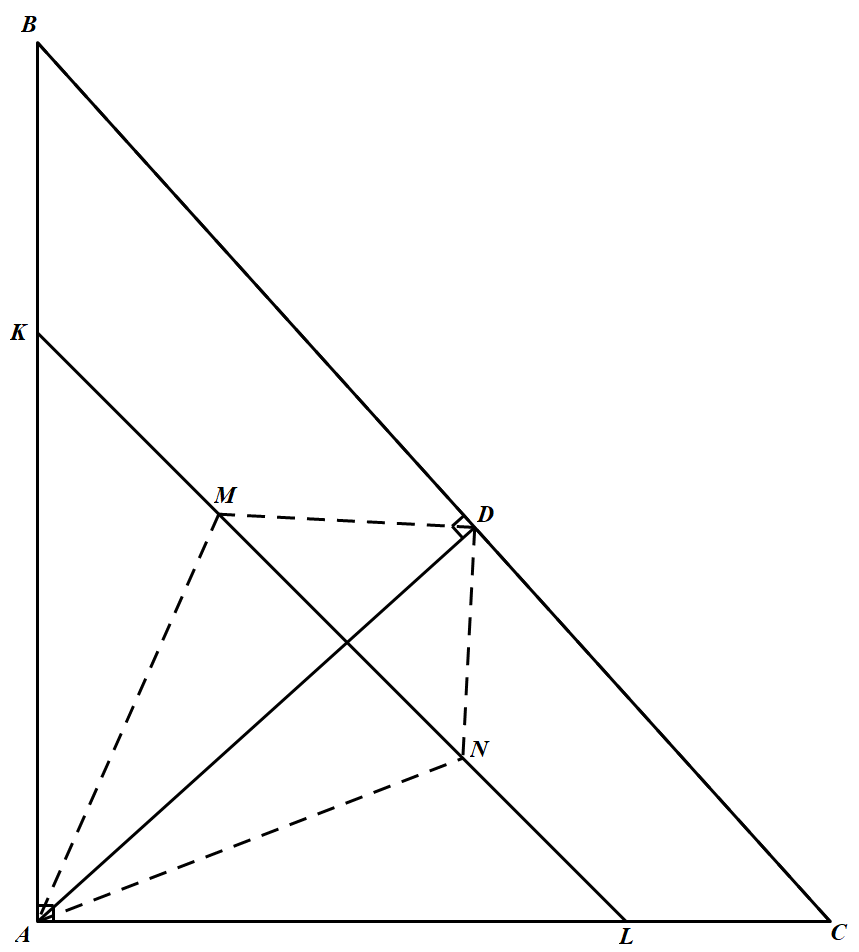
易见有 $\triangle ABC\sim\triangle DMN$．于是 $\angle B=\angle NMD$，即 $B,K,M,D$ 共圆．
于是，有 $\angle AKL=\angle BDM=45^\circ=\angle ADM$．
又 $\angle KAM=\angle DAM,AM=AM$，故有 $\triangle AMK\cong\triangle AMD$，于是 $AK=AD$．
同理，$AL=AD$．
于是，$S=\dfrac{1}{2}AB\cdot AC$；
$\begin{aligned}
T&=\frac{1}{2}AD^2=\frac{1}{2}\frac{AB^2\cdot AC^2}{BC^2}\\
&=\frac{AB^2\cdot AC^2}{2(AB^2+AC^2)}
\end{aligned}$
因此，$\dfrac{AB^2\cdot AC^2}{2AB\cdot AC}\geqslant 1$，即 $S\geqslant 2T$．
等号成立，仅当 $AB=AC$ 时．
易见有 $\triangle ABC\sim\triangle DMN$．于是 $\angle B=\angle NMD$，即 $B,K,M,D$ 共圆．于是，有 $\angle AKL=\angle BDM=45^\circ=\angle ADM$．
又 $\angle KAM=\angle DAM,AM=AM$，故有 $\triangle AMK\cong\triangle AMD$，于是 $AK=AD$．
同理，$AL=AD$．
于是，$S=\dfrac{1}{2}AB\cdot AC$；
$\begin{aligned}
T&=\frac{1}{2}AD^2=\frac{1}{2}\frac{AB^2\cdot AC^2}{BC^2}\\
&=\frac{AB^2\cdot AC^2}{2(AB^2+AC^2)}
\end{aligned}$
因此，$\dfrac{AB^2\cdot AC^2}{2AB\cdot AC}\geqslant 1$，即 $S\geqslant 2T$．
等号成立，仅当 $AB=AC$ 时．
答案
解析
备注
