设 $n$ 为一个正整数,而 ${A}_{1},{A}_{2},\cdots,{A}_{2n+1}$ 是集合 $B$ 的一族子集,满足条件:
(1)每个 ${A}_{i}$ 中恰有 $2n$ 个元素;
(2)${A}_{i}∩{A}_{j}(1\leqslant i<j\leqslant 2n+1)$ 恰含有一个元素;
(3)$B$ 中每一个元素至少属于两个子集 ${A}_{i_1}$ 和 $A_{i_2}$,$1\leqslant i_1<i_2\leqslant 2n+1$.
试问对怎样的 正整数 $n$,可以对 $B$ 中的每一个元素贴一张写有 $0$ 或 $1$ 的标签,使得每个 $A_i$ 中恰好有 $n$ 个贴上了写有 $0$ 的标签的元素?说明理由.(捷克斯洛伐克)
(1)每个 ${A}_{i}$ 中恰有 $2n$ 个元素;
(2)${A}_{i}∩{A}_{j}(1\leqslant i<j\leqslant 2n+1)$ 恰含有一个元素;
(3)$B$ 中每一个元素至少属于两个子集 ${A}_{i_1}$ 和 $A_{i_2}$,$1\leqslant i_1<i_2\leqslant 2n+1$.
试问对怎样的 正整数 $n$,可以对 $B$ 中的每一个元素贴一张写有 $0$ 或 $1$ 的标签,使得每个 $A_i$ 中恰好有 $n$ 个贴上了写有 $0$ 的标签的元素?说明理由.(捷克斯洛伐克)
【难度】
【出处】
1988年第29届IMO试题
【标注】
【答案】
略
【解析】
证法一
当且仅当 $n$ 为偶数时,有符合要求的贴标签的方式.
首先证明,由条件(1),(2),(3)可以得到比条件(3)更强的结论:$B$ 中的每一个元素恰好属于某两个子集 $A_i(1\leqslant i\leqslant 2n+1)$.
事实上,若 $B$ 中有一个元素 $a$ 至少属于 $3$ 个以上的子集,不妨设 $a\in A_1\bigcap A_2\bigcap A_3$,由条件(2),剩下的 $2n-2$ 个子集 $A_4,\cdots,A_{2n+1}$ 每一个至多含 $A_1$ 的一个元素,从而 $A_1$ 中至少有一个元素不属于 $A_2\bigcup A_3\bigcup \cdots A_{2n+1}$,与条件(3)矛盾.
于是,对满足条件(1),(2),(3)的集合 $B$,它的每一个元素都可与一个二元正整数组对应,即:若 $a\in B$,且 $a\in A_i\bigcap A_j(1\leqslant i<j\leqslant 2n+1)$,则令 $a$ 与无序对 $(i,j)$ 相对应.
若能按照题设要求贴上标签 $0$ 或 $1$,则在上述数组中,恰有一半与 $0$ 相对应,故有 $\dfrac{1}{2}C_{2n+1}^2=\dfrac{n(2n+1)}{2}$ 个 $0$,因此 $2|n(2n+1)$,所以 $n$ 为偶数.
又当 $n$ 为偶数时,我们可以构造出一种合乎要求的贴签方法.把一个圆周用 $2n+1$ 个点等分成 $2n+1$ 份.在这些点上依次标上数字 $1,2,\cdots,2n+1$.对于 $\{1,2,\cdots,2n+1\}$ 中任何两个不同的数 $i,j$,考虑它们在圆周上较短的那一段弧,若 $i$ 与 $j$ 之间隔着奇数段弧,则给 $A_i\bigcap A_j$ 中的那个元素贴上标签 $1$,若 $i$ 与 $j$ 之间隔着偶数段弧,则给 $A_i\bigcap A_j$ 中的那个元素贴上标签 $0$.由于 $n$ 是偶数,因此 $A_i$ 中的元素有一半贴上了 $0$,一半贴上了 $1$.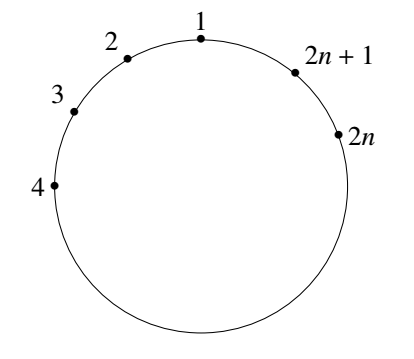 证法二
证法二
由题设条件可知,每个 $A_i$ 中的 $2n$ 个元素恰是它与另外 $2n$ 个子集的每一个各一个公共元素,且 $B=A_1\bigcup A_2\bigcup \cdots\bigcup A_{2n+1}$,于是 $B$ 的元素可排成一个 $2n\times 2n$ 的对称矩阵 $(a_{ij})$,其中 $a_{ij}=a_{ji}=A_i\bigcap A_j(1\leqslant i<j\leqslant 2n),a_{ij}=A_i\bigcap A_{2n+1}(1\leqslant i\leqslant 2n)$,矩阵 $(a_{ij})$ 的第 $i$ 行(或列)是 $A_i$,主对角线是 $A_{2n+1}$.
若能按照题设要求贴上标签 $0$ 或 $1$,则矩阵 $(a_{ij})$ 中共有 $2n\cdot n=2n^2$ 个 $0$,又因为是对称矩阵,故主对角线外的 $0$ 的个数是偶数个.因此对角线上也有偶数个 $0$,即 $n$ 是偶数.
另一方面,对于 $n=2k$,将 $4\times 4$ 矩阵:
$T=\begin{pmatrix}0 & 1&0&1 \\1&0&1&0\\0&1&1&0\\1&0&0&1\end{pmatrix}$
重复排列得到 $2n\times 2n$ 对称矩阵:
$\begin{pmatrix}T& T&\cdots&T \\T&T&\cdots&T\\\vdots&\vdots&\ddots&\vdots\\T&T&\cdots&T\end{pmatrix}$
按这个矩阵给 $B$ 的元素贴标签,可满足题意.
当且仅当 $n$ 为偶数时,有符合要求的贴标签的方式.
首先证明,由条件(1),(2),(3)可以得到比条件(3)更强的结论:$B$ 中的每一个元素恰好属于某两个子集 $A_i(1\leqslant i\leqslant 2n+1)$.
事实上,若 $B$ 中有一个元素 $a$ 至少属于 $3$ 个以上的子集,不妨设 $a\in A_1\bigcap A_2\bigcap A_3$,由条件(2),剩下的 $2n-2$ 个子集 $A_4,\cdots,A_{2n+1}$ 每一个至多含 $A_1$ 的一个元素,从而 $A_1$ 中至少有一个元素不属于 $A_2\bigcup A_3\bigcup \cdots A_{2n+1}$,与条件(3)矛盾.
于是,对满足条件(1),(2),(3)的集合 $B$,它的每一个元素都可与一个二元正整数组对应,即:若 $a\in B$,且 $a\in A_i\bigcap A_j(1\leqslant i<j\leqslant 2n+1)$,则令 $a$ 与无序对 $(i,j)$ 相对应.
若能按照题设要求贴上标签 $0$ 或 $1$,则在上述数组中,恰有一半与 $0$ 相对应,故有 $\dfrac{1}{2}C_{2n+1}^2=\dfrac{n(2n+1)}{2}$ 个 $0$,因此 $2|n(2n+1)$,所以 $n$ 为偶数.
又当 $n$ 为偶数时,我们可以构造出一种合乎要求的贴签方法.把一个圆周用 $2n+1$ 个点等分成 $2n+1$ 份.在这些点上依次标上数字 $1,2,\cdots,2n+1$.对于 $\{1,2,\cdots,2n+1\}$ 中任何两个不同的数 $i,j$,考虑它们在圆周上较短的那一段弧,若 $i$ 与 $j$ 之间隔着奇数段弧,则给 $A_i\bigcap A_j$ 中的那个元素贴上标签 $1$,若 $i$ 与 $j$ 之间隔着偶数段弧,则给 $A_i\bigcap A_j$ 中的那个元素贴上标签 $0$.由于 $n$ 是偶数,因此 $A_i$ 中的元素有一半贴上了 $0$,一半贴上了 $1$.
 证法二
证法二由题设条件可知,每个 $A_i$ 中的 $2n$ 个元素恰是它与另外 $2n$ 个子集的每一个各一个公共元素,且 $B=A_1\bigcup A_2\bigcup \cdots\bigcup A_{2n+1}$,于是 $B$ 的元素可排成一个 $2n\times 2n$ 的对称矩阵 $(a_{ij})$,其中 $a_{ij}=a_{ji}=A_i\bigcap A_j(1\leqslant i<j\leqslant 2n),a_{ij}=A_i\bigcap A_{2n+1}(1\leqslant i\leqslant 2n)$,矩阵 $(a_{ij})$ 的第 $i$ 行(或列)是 $A_i$,主对角线是 $A_{2n+1}$.
若能按照题设要求贴上标签 $0$ 或 $1$,则矩阵 $(a_{ij})$ 中共有 $2n\cdot n=2n^2$ 个 $0$,又因为是对称矩阵,故主对角线外的 $0$ 的个数是偶数个.因此对角线上也有偶数个 $0$,即 $n$ 是偶数.
另一方面,对于 $n=2k$,将 $4\times 4$ 矩阵:
$T=\begin{pmatrix}0 & 1&0&1 \\1&0&1&0\\0&1&1&0\\1&0&0&1\end{pmatrix}$
重复排列得到 $2n\times 2n$ 对称矩阵:
$\begin{pmatrix}T& T&\cdots&T \\T&T&\cdots&T\\\vdots&\vdots&\ddots&\vdots\\T&T&\cdots&T\end{pmatrix}$
按这个矩阵给 $B$ 的元素贴标签,可满足题意.
答案
解析
备注