锐角 $\triangle ABC$ 中，$\angle A$ 的平分线交 $BC$ 于 $L$，交 $\triangle ABC$ 的外接圆于 $N$，$LK\perp AB$ 交 $AB$ 于 $K$，$LM\perp AC$ 交与 $M$．求证：$S_{\triangle ABC}=S_{四边形 AKNM}$．（苏联）
【难度】
【出处】
1987年第28届IMO试题
【标注】
【答案】
略
【解析】
证法一
如图，作 $\triangle ABC$ 的高 $AH$，则 $A,K,H,L,M$ 五点共圆．联结 $KH,HM,HN,BN$ 和 $NC$．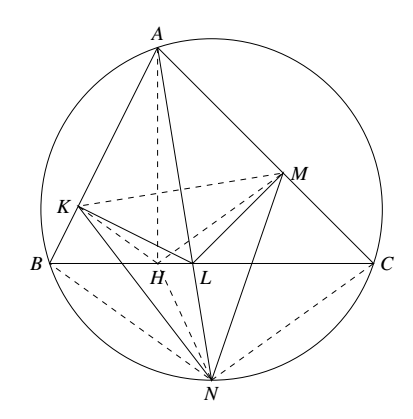
$\begin{aligned}
\angle KHB&=\angle BAN\\
&=\angle NAC\\
&=\angle NBC
\end{aligned}$
于是 $KH\parallel BN$，故 $S_{\triangle KHN}=S_{\triangle BKH}$，同理有 $S_{\triangle MHN}=S_{\triangle HMC}$．
由此即得 $S_{\triangle ABC}=S_{四边形AKNM}$．
证法二
延用证法一的图，联结 $KM$，易知 $AN$ 垂直平分 $KM$．
由 $A,K,L,M$ 共圆及正弦定理，知
$S_{四边形AKNM}=\dfrac{1}{2}KM\cdot AN=\dfrac{1}{2}AL\cdot AN\cdot \sin\angle BAC$
而 $S_{\triangle ABC}=\dfrac{1}{2}AB\cdot AC\cdot \sin\angle BAC$．
欲证两者面积相等，只须证明 $AL\cdot AN=AB\cdot AC$
下面证明之．
由于 $\angle BAL=\angle NAC,\angle ABL=\angle ANC$
故 $\triangle ABL\sim\triangle ANC$．
于是 $\dfrac{AB}{AL}=\dfrac{AN}{AC}$
此即 $AL\cdot AN=AB\cdot AC$
如图，作 $\triangle ABC$ 的高 $AH$，则 $A,K,H,L,M$ 五点共圆．联结 $KH,HM,HN,BN$ 和 $NC$．
$\begin{aligned}\angle KHB&=\angle BAN\\
&=\angle NAC\\
&=\angle NBC
\end{aligned}$
于是 $KH\parallel BN$，故 $S_{\triangle KHN}=S_{\triangle BKH}$，同理有 $S_{\triangle MHN}=S_{\triangle HMC}$．
由此即得 $S_{\triangle ABC}=S_{四边形AKNM}$．
证法二
延用证法一的图，联结 $KM$，易知 $AN$ 垂直平分 $KM$．
由 $A,K,L,M$ 共圆及正弦定理，知
$S_{四边形AKNM}=\dfrac{1}{2}KM\cdot AN=\dfrac{1}{2}AL\cdot AN\cdot \sin\angle BAC$
而 $S_{\triangle ABC}=\dfrac{1}{2}AB\cdot AC\cdot \sin\angle BAC$．
欲证两者面积相等，只须证明 $AL\cdot AN=AB\cdot AC$
下面证明之．
由于 $\angle BAL=\angle NAC,\angle ABL=\angle ANC$
故 $\triangle ABL\sim\triangle ANC$．
于是 $\dfrac{AB}{AL}=\dfrac{AN}{AC}$
此即 $AL\cdot AN=AB\cdot AC$
答案
解析
备注
