以 $O$ 为 中心的正 $n(n\geqslant 5)$ 边形 的两个相邻顶点标记为 $A$ 和 $B$．$\triangle XYZ\cong\triangle OAB$．最初令 $\triangle XYZ$ 重合于 $\triangle OAB$，然后在平面上移动 $\triangle XYZ$，使得点 $Y、Z$ 都沿着多边形的周界移动而点 $X$ 在多边形内部移动，求点 $X$ 的运动轨迹．（以色列）
【难度】
【出处】
1986年第27届IMO试题
【标注】
【答案】
略
【解析】
设正 $n$ 边形外接圆半径为 $R$．如图所示．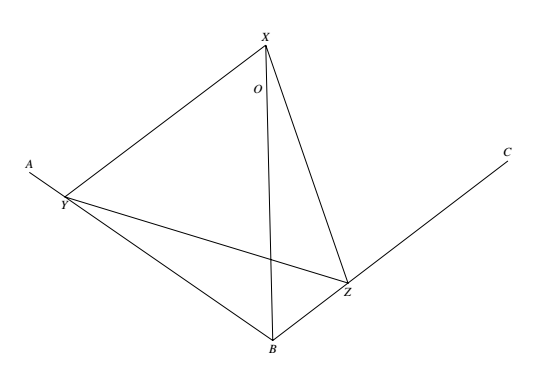
由正多边形的对称性，只要考虑 $\triangle XYZ$ 由 $\triangle OAB$ 位置移动到 $\triangle OBC$（$A,B,C$ 是正 $n$ 边形连续三顶点）位置时 $X$ 的轨迹．
易知，有
$\angle YXZ=\angle AOB=180^\circ-2\angle OBA=180^\circ-\angle ABC$．
因此 $X,Y,B,Z$ 共圆，于是 $\angle XBY=\angle XZY=\angle OBA$，于是 $X,O,B$ 三点共线．
由正弦定理，
$\begin{aligned}
BX&=\frac{YZ}{\sin\angle ABC}\cdot\sin\angle XYB\\
&\leqslant\frac{AB}{\sin\angle AOB}=\frac{2R\sin\frac{180^circ}{n}}{\sin\frac{360^\circ}{n}}\\
&=R\sec\frac{180^\circ}{n}
\end{aligned}$
等号成立，仅当 $\angle XYB=\angle XZB=90^\circ$，这时 $XB$ 正好垂直平分 $YZ$．
由连续性及对称性知，所求轨迹为以 $O$ 为中心的 $n$ 段射线组成的"星形"，它们同 $O$ 与个顶点的联线方向相反，长度是 $R\left(\sec\dfrac{180^\circ}{n}-1\right)$．
由正多边形的对称性，只要考虑 $\triangle XYZ$ 由 $\triangle OAB$ 位置移动到 $\triangle OBC$（$A,B,C$ 是正 $n$ 边形连续三顶点）位置时 $X$ 的轨迹．易知，有
$\angle YXZ=\angle AOB=180^\circ-2\angle OBA=180^\circ-\angle ABC$．
因此 $X,Y,B,Z$ 共圆，于是 $\angle XBY=\angle XZY=\angle OBA$，于是 $X,O,B$ 三点共线．
由正弦定理，
$\begin{aligned}
BX&=\frac{YZ}{\sin\angle ABC}\cdot\sin\angle XYB\\
&\leqslant\frac{AB}{\sin\angle AOB}=\frac{2R\sin\frac{180^circ}{n}}{\sin\frac{360^\circ}{n}}\\
&=R\sec\frac{180^\circ}{n}
\end{aligned}$
等号成立，仅当 $\angle XYB=\angle XZB=90^\circ$，这时 $XB$ 正好垂直平分 $YZ$．
由连续性及对称性知，所求轨迹为以 $O$ 为中心的 $n$ 段射线组成的"星形"，它们同 $O$ 与个顶点的联线方向相反，长度是 $R\left(\sec\dfrac{180^\circ}{n}-1\right)$．
答案
解析
备注
