设四边形 $ABCD$ 内接于圆，另一圆的圆心在边 $AB$ 上且与四边形的其余三条边均相切．求证：$AD+BC=AB$．（英国）
【难度】
【出处】
1985年第26届IMO试题
【标注】
【答案】
略
【解析】
证法一
如图，设 $AB$ 上的圆心为 $O$，$\odot O$ 分别与 $AD,DC,CB$ 相切于 $E,F,G$．联结 $OE,OF,OG$，易知 $OE=OF=OG$．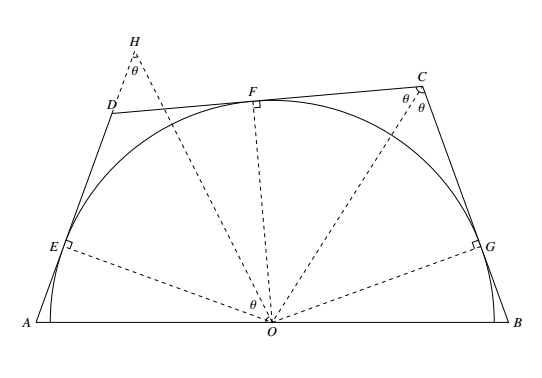
设 $\angle DCB=2\theta$，则 $\angle FCO=\theta$．将 $\triangle OFC$ 绕 $O$ 点旋转得到 $\triangle OEH$．$H$ 在 $AD$ 直线上，由 $A,B,C,D$ 共圆，$\angle A=180^\circ-2\theta$．于是 $\angle HOA=180^\circ-\angle A-\theta=\theta=\angle AHO$，因此 $AO=AH=AE+FC=AE+CG$．
同理可证 $BO=BG+ED$．
两式一加，即得 $AB=AD+BC$．
证法二
不妨设 $\angle B\leqslant \angle A$．联结 $OD,OC$．
$\begin{aligned}
\angle AOD&=180^\circ-\angle A-\angle ADO\\
&=90^\circ+\frac{\angle B}{2}-\angle A\\
&\leqslant 90^\circ-\frac{\angle B}{2}\\
&=\angle ADO
\end{aligned}$
于是 $AD\leqslant AO$．如图，在 $AO$ 内取一点 $E$，使 $AD=AE$，显然接下来就是要证明 $BE=BC$ 即可．联结 $DE,CE$．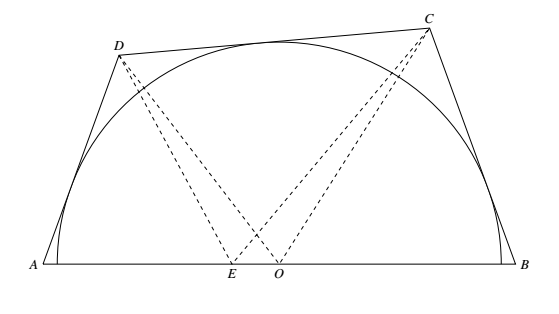
易见
$\begin{aligned}
\angle AED&=90^\circ-\frac{\angle A}{2}\\
&=\frac{\angle DCB}{2}\\
&=\angle DCO
\end{aligned}$
于是 $D,E,O,C$ 四点共圆，于是
$\begin{aligned}
\angle CEB&=\angle ODC\\
&=\frac{\angle ADC}{2}\\
&=90^\circ-\frac{\angle B}{2}
\end{aligned}$
$\begin{aligned}
\angle ECB&=180^\circ -\angle CEB-\angle B\\
&=90^\circ-\frac{\angle B}{2}\\
&=\angle CEB
\end{aligned}$
于是 $BE=BC$．
如图，设 $AB$ 上的圆心为 $O$，$\odot O$ 分别与 $AD,DC,CB$ 相切于 $E,F,G$．联结 $OE,OF,OG$，易知 $OE=OF=OG$．
设 $\angle DCB=2\theta$，则 $\angle FCO=\theta$．将 $\triangle OFC$ 绕 $O$ 点旋转得到 $\triangle OEH$．$H$ 在 $AD$ 直线上，由 $A,B,C,D$ 共圆，$\angle A=180^\circ-2\theta$．于是 $\angle HOA=180^\circ-\angle A-\theta=\theta=\angle AHO$，因此 $AO=AH=AE+FC=AE+CG$．同理可证 $BO=BG+ED$．
两式一加，即得 $AB=AD+BC$．
证法二
不妨设 $\angle B\leqslant \angle A$．联结 $OD,OC$．
$\begin{aligned}
\angle AOD&=180^\circ-\angle A-\angle ADO\\
&=90^\circ+\frac{\angle B}{2}-\angle A\\
&\leqslant 90^\circ-\frac{\angle B}{2}\\
&=\angle ADO
\end{aligned}$
于是 $AD\leqslant AO$．如图，在 $AO$ 内取一点 $E$，使 $AD=AE$，显然接下来就是要证明 $BE=BC$ 即可．联结 $DE,CE$．
易见$\begin{aligned}
\angle AED&=90^\circ-\frac{\angle A}{2}\\
&=\frac{\angle DCB}{2}\\
&=\angle DCO
\end{aligned}$
于是 $D,E,O,C$ 四点共圆，于是
$\begin{aligned}
\angle CEB&=\angle ODC\\
&=\frac{\angle ADC}{2}\\
&=90^\circ-\frac{\angle B}{2}
\end{aligned}$
$\begin{aligned}
\angle ECB&=180^\circ -\angle CEB-\angle B\\
&=90^\circ-\frac{\angle B}{2}\\
&=\angle CEB
\end{aligned}$
于是 $BE=BC$．
答案
解析
备注
