设以 $O$ 为心的圆经过 $\triangle ABC$ 的两个顶点 $A$ 和 $C$，且与边 $AB,BC$ 分别交于 $K$ 和 $N$，点 $K$ 与 $N$ 不同，又设 $\triangle ABC$ 和 $\triangle KBN$ 的外接圆交于 $B$ 和另一点 $M$．求证：$\angle OMB$ 是直角．（苏联）
【难度】
【出处】
1985年第26届IMO试题
【标注】
【答案】
略
【解析】
证法一
如图，三圆两两相交，直线 $AC,KN$ 和 $BM$ 是三条根轴．由条件（$K$ 与 $N$ 不同；$B$ 与 $M$ 不同）知三条根轴必交于一点，即根心 $P$，它对于三圆的幂是相等的．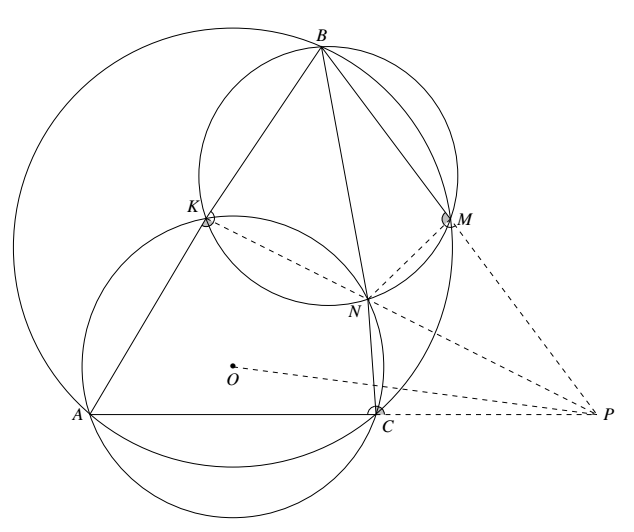
易知 $\angle PMN=\angle BKN=\angle NCA$，故 $M,N,C,P$ 四点共圆．
于是，$BM\cdot BP=BN\cdot BC=BO^2-r^2$ ①
$PM\cdot PB=PN\cdot PK=PO^2-r^2$ ②
这里 $r$ 为 $\odot O$ 之半径．
① $-$ ② 得
$\begin{aligned}
BO^2-PO^2&=BP(BM-PM)\\
&=(BM+PM)(BM-PM)\\
&=BM^2-PM^2
\end{aligned}$
因此 $OM\perp BP$．
证法二
如图，设 $\triangle ABC$ 与 $\triangle BKN$ 的外接圆圆心分别是 $O_1,O_2$．联结 $KN,O_1B,O_1O,OO_2,O_1O_2,BO_2$ 和 $MO_2$．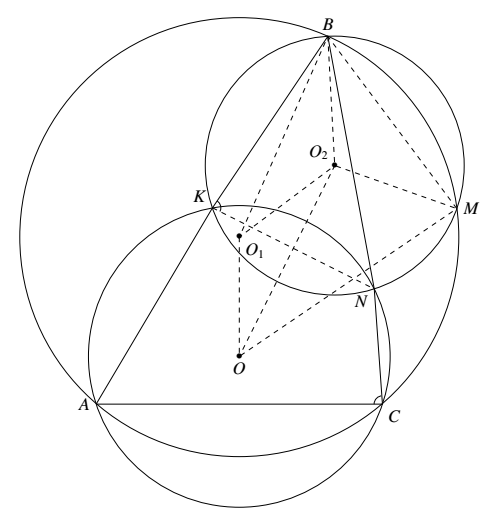
一个熟知的结论是 $BO_1\perp KN$，这是因为
$\begin{aligned}
\angle O_1BA&=90^\circ-\frac{1}{2}\angle BO_1A\\
&=90^\circ-\angle BCA\\
&=90^\circ-\angle BKN
\end{aligned}$
同理有 $BO_2\perp AC$．
由于 $OO_2\perp KN$，故 $BO_1\parallel O_1O_2$，同理有 $BO_2\parallel O_1O$．因此四边形 $BO_1OO_2$ 为平行四边形．又 $O_1O_2$ 垂直平分 $BM$，于是推得
（1）$MO_2=BO_2=O_1O$；
（2）$\angle OO_1O_2=\angle BO_2O_1=\angle MO_2O_1$．
于是四边形 $O_1OMO_2$ 为等腰梯形，于是由 $OM\parallel O_1O_2$ 及 $O_1O_2\perp BM$ 立知 $\angle OMB=90^\circ$．
证法三
如图，联结 $KN$．延长 $MN$ 交 $\odot O$ 于另一点 $D$，联结 $AD$．
易知 $\angle MDA=\angle BKN=180^\circ-\angle BMD$．
因此 $AD\parallel BM$．
如果我们能证明 $MO\perp AD$，则结论马上成立．
又易知 $OA=OD$，即 $O$ 在 $AD$ 之垂直平分线上．如能证明 $M$ 也在 $AD$ 之垂直平分线上，则 $MO\perp AD$．于是问题归结为证明 $AM=DM$．
下面我们就来证明之．
由一系列四点共圆知：
$\begin{aligned}
\angle MAD&=\angle MAC+\angle DAC\\
&=\angle MBC+\angle DNC\\
&=\angle MBN+\angle MNB\\
&=180^\circ-\angle BMN\\
&=\angle BKN-\angle BCA\\
&=\angle MDA
\end{aligned}$
因此 $AM=DM$ 成立．
于是 $\angle OMB=90^\circ$．
如图，三圆两两相交，直线 $AC,KN$ 和 $BM$ 是三条根轴．由条件（$K$ 与 $N$ 不同；$B$ 与 $M$ 不同）知三条根轴必交于一点，即根心 $P$，它对于三圆的幂是相等的．
易知 $\angle PMN=\angle BKN=\angle NCA$，故 $M,N,C,P$ 四点共圆．于是，$BM\cdot BP=BN\cdot BC=BO^2-r^2$ ①
$PM\cdot PB=PN\cdot PK=PO^2-r^2$ ②
这里 $r$ 为 $\odot O$ 之半径．
① $-$ ② 得
$\begin{aligned}
BO^2-PO^2&=BP(BM-PM)\\
&=(BM+PM)(BM-PM)\\
&=BM^2-PM^2
\end{aligned}$
因此 $OM\perp BP$．
证法二
如图，设 $\triangle ABC$ 与 $\triangle BKN$ 的外接圆圆心分别是 $O_1,O_2$．联结 $KN,O_1B,O_1O,OO_2,O_1O_2,BO_2$ 和 $MO_2$．
一个熟知的结论是 $BO_1\perp KN$，这是因为$\begin{aligned}
\angle O_1BA&=90^\circ-\frac{1}{2}\angle BO_1A\\
&=90^\circ-\angle BCA\\
&=90^\circ-\angle BKN
\end{aligned}$
同理有 $BO_2\perp AC$．
由于 $OO_2\perp KN$，故 $BO_1\parallel O_1O_2$，同理有 $BO_2\parallel O_1O$．因此四边形 $BO_1OO_2$ 为平行四边形．又 $O_1O_2$ 垂直平分 $BM$，于是推得
（1）$MO_2=BO_2=O_1O$；
（2）$\angle OO_1O_2=\angle BO_2O_1=\angle MO_2O_1$．
于是四边形 $O_1OMO_2$ 为等腰梯形，于是由 $OM\parallel O_1O_2$ 及 $O_1O_2\perp BM$ 立知 $\angle OMB=90^\circ$．
证法三
如图，联结 $KN$．延长 $MN$ 交 $\odot O$ 于另一点 $D$，联结 $AD$．
易知 $\angle MDA=\angle BKN=180^\circ-\angle BMD$．因此 $AD\parallel BM$．
如果我们能证明 $MO\perp AD$，则结论马上成立．
又易知 $OA=OD$，即 $O$ 在 $AD$ 之垂直平分线上．如能证明 $M$ 也在 $AD$ 之垂直平分线上，则 $MO\perp AD$．于是问题归结为证明 $AM=DM$．
下面我们就来证明之．
由一系列四点共圆知：
$\begin{aligned}
\angle MAD&=\angle MAC+\angle DAC\\
&=\angle MBC+\angle DNC\\
&=\angle MBN+\angle MNB\\
&=180^\circ-\angle BMN\\
&=\angle BKN-\angle BCA\\
&=\angle MDA
\end{aligned}$
因此 $AM=DM$ 成立．
于是 $\angle OMB=90^\circ$．
答案
解析
备注
