已知 $\triangle {A}_{1}{A}_{2}{A}_{3}$ 为不等边 三角形，它的三边分别为 ${a}_{1}、{a}_{2}、{a}_{3}$，其中 ${a}_{i}$ 是 ${A}_{i}$ 的对边 $(i=1,2,3)$，${M}_{i}$ 是边 ${a}_{i}$ 的中点，${T}_{i}$ 为 $\triangle {A}_{1}{A}_{2}{A}_{3}$ 内切圆与 ${a}_{i}$ 边 的切点，${S}_{i}$ 是 ${T}_{i}$ 关于 $\angle {A}_{i}$ 平分线的对称点．求证：${M}_{1}{S}_{1}、{M}_{2}{S}_{2}、{M}_{3}{S}_{3}$ 三线共点．（荷兰）
【难度】
【出处】
1982年第23届IMO试题
【标注】
【答案】
略
【解析】
如图，设 $A_1B_1,A_2B_2,A_3B_3$ 为三条角平分线，$B_i$ 在 $a_i$ 上．$I$ 是内心．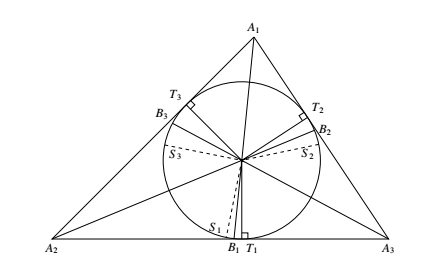
$\angle T_2B_2I=\dfrac{1}{2}\angle A_2+\angle A_3$
所以 $\angle T_2IB_2=\angle S_2IB_2=90^\circ-\dfrac{1}{2}\angle A_2-\angle A_3$．
于是
$\begin{aligned}
\angle S_2IT_2&=\angle T_2IT_1-2\angle T_2IB_2\\
&=180^\circ-\angle A_3-(180^\circ-\angle A_2-2\angle A_3)\\
&=\angle A_2+\angle A_3
\end{aligned}$
同理，$\angle S_3IT_1=\angle A_2+\angle A_3$
由于 $IT_1\perp A_2A_3$ 及 $IS_2=IS_3$（易证：$S_1,S_2,S_3$ 在内切圆上），故有 $S_2S_3\parallel A_2A_3$，类似可得，$S_3S_1\parallel A_3A_1$ 和 $S_1S_2\parallel A_1A_2$．
于是 $\triangle S_1S_2S_3$ 和 $\triangle M_1M_2M_3$（未画出）的各相应边平行．由于 $\triangle A_1A_2A_3$ 是不等边三角形，$\triangle S_1S_2S_3$ 和 $\triangle M_1M_2M_3$ 无重合顶点，故 $M_1S_1,M_2S_2,M_3S_3$ 共点．
$\angle T_2B_2I=\dfrac{1}{2}\angle A_2+\angle A_3$所以 $\angle T_2IB_2=\angle S_2IB_2=90^\circ-\dfrac{1}{2}\angle A_2-\angle A_3$．
于是
$\begin{aligned}
\angle S_2IT_2&=\angle T_2IT_1-2\angle T_2IB_2\\
&=180^\circ-\angle A_3-(180^\circ-\angle A_2-2\angle A_3)\\
&=\angle A_2+\angle A_3
\end{aligned}$
同理，$\angle S_3IT_1=\angle A_2+\angle A_3$
由于 $IT_1\perp A_2A_3$ 及 $IS_2=IS_3$（易证：$S_1,S_2,S_3$ 在内切圆上），故有 $S_2S_3\parallel A_2A_3$，类似可得，$S_3S_1\parallel A_3A_1$ 和 $S_1S_2\parallel A_1A_2$．
于是 $\triangle S_1S_2S_3$ 和 $\triangle M_1M_2M_3$（未画出）的各相应边平行．由于 $\triangle A_1A_2A_3$ 是不等边三角形，$\triangle S_1S_2S_3$ 和 $\triangle M_1M_2M_3$ 无重合顶点，故 $M_1S_1,M_2S_2,M_3S_3$ 共点．
答案
解析
备注
