已知 $AC,CE$ 是正六边形 $ABCDEF$ 的两条对角线，点 $M,N$ 分别内分 $AC,CE$，且使 $\dfrac{AM}{AC}=\dfrac{CN}{CE}=r$．如果 $B、M、N$ 三点共线，求 $r$ 的值．（荷兰）
【难度】
【出处】
1982年第23届IMO试题
【标注】
【答案】
略
【解析】
证法一
如图，联结 $DN$．易知 $AM=CN,\triangle AMB\cong\triangle CND$．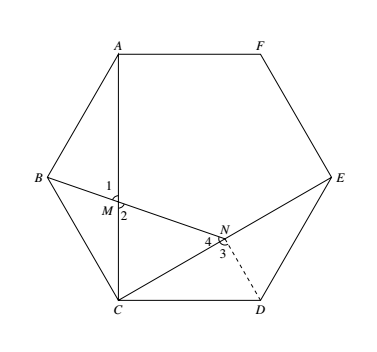
于是
$\begin{aligned}
\angle BND&=\angle 3+\angle 4\\
&=\angle 1+\angle 4\\
&=\angle 2+\angle 4\\
&=180^circ-\angle ACE\\
&=120^\circ
\end{aligned}$
由于 $\angle BCD=120^circ,CB=CD$，以 $C$ 为圆心，$BC$ 为半径作圆，与 $C$ 在弦 $BD$ 同侧的圆周角为 $60^\circ$，与 $C$ 在弦 $BD$ 异侧的圆周角为 $120^\circ$，$N$ 正好满足，于是 $N$ 在该圆上，$CN=CD$．
于是 $r=\dfrac{CN}{CE}=\dfrac{CD}{CE}=\dfrac{\sqrt{3}}{3}$．
证法二
设正六边形 $ABCDEF$ 边长为 $1$，如图联结 $BE$ 交 $AC$ 于 $G$，易知 $BE=2,GB=\dfrac{1}{2}$．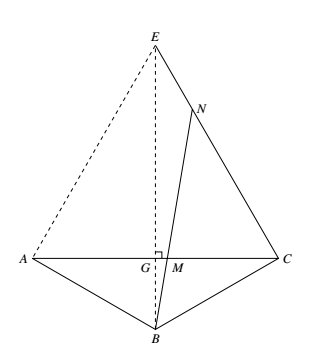
$\begin{aligned}
CE&=\sqrt{3}\\
CN&=\sqrt{3}r\\
CM=EN&=\sqrt{3}(1-r)\\
GM&=\dfrac{1}{2}AC-CM\\
&=\dfrac{\sqrt{3}}{2}-\sqrt{3}(1-r)\\
&=\dfrac{\sqrt{3}}{2}(2r-1)
\end{aligned}$
由条件知有梅内劳斯定理：$\dfrac{EB}{BG}\cdot \dfrac{GM}{MC}\cdot \dfrac{CN}{NE}=1$．
代入，得方程 $\dfrac{2r-1}{2(1-r)}\cdot\dfrac{r}{1-r}=\dfrac{1}{4}$．
解得 $r=\dfrac{1}{\sqrt{3}}$．
如图，联结 $DN$．易知 $AM=CN,\triangle AMB\cong\triangle CND$．
于是$\begin{aligned}
\angle BND&=\angle 3+\angle 4\\
&=\angle 1+\angle 4\\
&=\angle 2+\angle 4\\
&=180^circ-\angle ACE\\
&=120^\circ
\end{aligned}$
由于 $\angle BCD=120^circ,CB=CD$，以 $C$ 为圆心，$BC$ 为半径作圆，与 $C$ 在弦 $BD$ 同侧的圆周角为 $60^\circ$，与 $C$ 在弦 $BD$ 异侧的圆周角为 $120^\circ$，$N$ 正好满足，于是 $N$ 在该圆上，$CN=CD$．
于是 $r=\dfrac{CN}{CE}=\dfrac{CD}{CE}=\dfrac{\sqrt{3}}{3}$．
证法二
设正六边形 $ABCDEF$ 边长为 $1$，如图联结 $BE$ 交 $AC$ 于 $G$，易知 $BE=2,GB=\dfrac{1}{2}$．
$\begin{aligned}CE&=\sqrt{3}\\
CN&=\sqrt{3}r\\
CM=EN&=\sqrt{3}(1-r)\\
GM&=\dfrac{1}{2}AC-CM\\
&=\dfrac{\sqrt{3}}{2}-\sqrt{3}(1-r)\\
&=\dfrac{\sqrt{3}}{2}(2r-1)
\end{aligned}$
由条件知有梅内劳斯定理：$\dfrac{EB}{BG}\cdot \dfrac{GM}{MC}\cdot \dfrac{CN}{NE}=1$．
代入，得方程 $\dfrac{2r-1}{2(1-r)}\cdot\dfrac{r}{1-r}=\dfrac{1}{4}$．
解得 $r=\dfrac{1}{\sqrt{3}}$．
答案
解析
备注
