设 $P$ 为 $\triangle ABC$ 内一点,$D、E、F$ 分别为 $P$ 到 $BC、CA、AB$ 三边所引垂线的垂足,求使得表达式 $\dfrac{BC}{PD}+\dfrac{CA}{PE}+\dfrac{AB}{PF}$ 取 最小值的所有点 $P$.(英国)
【难度】
【出处】
1981年第22届IMO试题
【标注】
【答案】
略
【解析】
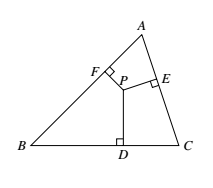 易知
易知$\begin{aligned}
&BC\cdot PD+CA\cdot PE+AB\cdot PF\\
&=2(S_{\triangle ABP}+S_{\triangle BCP}+S_{\triangle CAP})\\
&=2S_{\triangle ABC}
\end{aligned}$
设 $\dfrac{BC}{PD}+\dfrac{CA}{PE}+\dfrac{AB}{PF}=x$,则由柯西不等式,知
$\begin{aligned}
2xS_{\triangle ABC}&=(\dfrac{BC}{PD}+\dfrac{CA}{PE}+\dfrac{AB}{PF})(BC\cdot PD+CA\cdot PE+AB\cdot PF)\\
&\geqslant(BC+CA+AB)^2\\
&=C^2_{\triangle ABC}
\end{aligned}$
$C_{\triangle ABC}$ 为 $\triangle ABC$ 之周长.
柯西不等式等号成立的条件是 $PD=PE=PF$,于是,仅当 $P$ 是 $\triangle ABC$ 内心时,表达式最小值为 $\dfrac{C^2_{\triangle ABC}}{2S_{\triangle ABC}}$.
答案
解析
备注