已知三个等圆有一个公共点 $O$，并且都在一个已知三角形内．每一个圆与三角形的两边相切．求证：这个三角形的内心、外心与点 $O$ 共线．（苏联）
【难度】
【出处】
1981年第22届IMO试题
【标注】
【答案】
略
【解析】
将该三角形分别用 $A,B,C$ 表示．各圆圆心分别用 $A^\prime,B^\prime,C^\prime$ 表示，如图所示．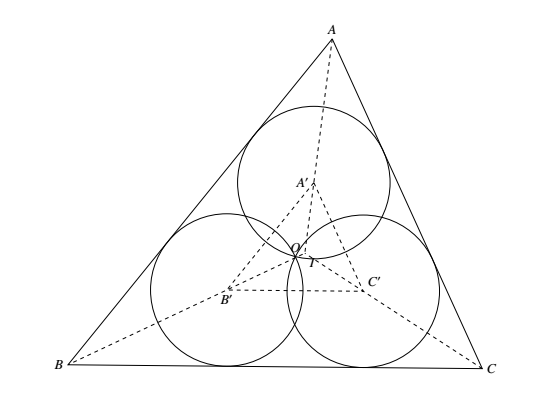
于是因三圆半径相等，$\triangle ABC$ 的各对应边与 $\triangle A^\prime B^\prime C^\prime$ 的相应各边平行．$AA^\prime$ 平分 $\angle BAC$，延长后也平分 $\angle B^\prime A^\prime C^\prime$，$BB^\prime,CC^\prime$ 也有类似性质．
于是 $\triangle ABC$ 的内心 $I$ 也是 $\triangle A^\prime B^\prime C^\prime$ 的内心，并同时是这两个三角形的位似中心．
位似的一个重要性质是各对应点与位似中心共线，既然 $O$ 是 $\triangle A^\prime B^\prime C^\prime$ 之外心，于是 $\triangle ABC$ 的外心 $O^\prime$，内心 $I$，点 $O$ 就必定共线．
于是因三圆半径相等，$\triangle ABC$ 的各对应边与 $\triangle A^\prime B^\prime C^\prime$ 的相应各边平行．$AA^\prime$ 平分 $\angle BAC$，延长后也平分 $\angle B^\prime A^\prime C^\prime$，$BB^\prime,CC^\prime$ 也有类似性质．于是 $\triangle ABC$ 的内心 $I$ 也是 $\triangle A^\prime B^\prime C^\prime$ 的内心，并同时是这两个三角形的位似中心．
位似的一个重要性质是各对应点与位似中心共线，既然 $O$ 是 $\triangle A^\prime B^\prime C^\prime$ 之外心，于是 $\triangle ABC$ 的外心 $O^\prime$，内心 $I$，点 $O$ 就必定共线．
答案
解析
备注
