平面上两圆相交，$A$ 为一个交点，两动点同时从 $A$ 出发，以匀速分别在各自的圆周上依相同方向绕行．旋转一周后，同时回到出发点．求证：在平面上存在一点 $P$，使得在任何时刻从 $P$ 到两动点的距离都相等．（苏联）
【难度】
【出处】
1979年第21届IMO试题
【标注】
【答案】
略
【解析】
证法一
由题设知两动点具有相同角速度．
如图，$\odot O_1$ 和 $\odot O_2$ 上分别有两动点 $Q_1$ 和 $Q_2$．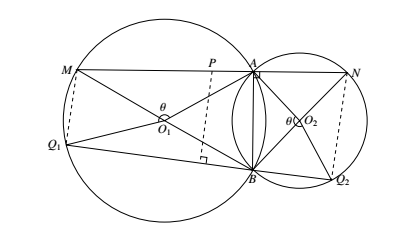
则有 $\angle AO_1Q_1=\angle AO_2Q_2$（设为 $\theta$）．
设两圆的另一个交点是 $B$，易知
$\angle ABQ_1=\dfrac{\theta}{2},\angle ABQ_2=180^\circ-\dfrac{\theta}{2}$，
于是 $\angle ABQ_1+\angle ABQ_2=180^\circ$，$Q_1,B,Q_2$ 共线．
过 $A$ 作 $MAN\perp AB$，其中 $M,N$ 分别在 $\odot O_1$ 和 $\odot O_2$ 上．于是 $\angle MQ_1Q_2=\angle NQ_2Q_1=90^\circ$，即四边形 $MQ_1Q_2N$ 为一直角梯形．这样 $Q_1Q_2$ 的中垂线过 $MN$ 中点，设其为 $P$．于是 $PQ_1=PQ_2$，$P$ 显然是所求之定点．
证法二
建立复平面，不妨设 $O_1$ 为原点，且圆 $O_1$ 半径为 $1$，$O_2$ 在实轴正半轴坐标为 $d$，设目前点转过的角度为 $\alpha$，$\alpha\in[0,2\pi)$，则点在圆 $O_1$ 位置 $M_1$ 为 $\cos(\theta+\alpha)+{\rm{i}\sin(\theta+\alpha)}$，点在圆 $O_2$ 的位置 $M_2$ 为 $d+(\cos\theta+{\rm{i}}\sin\theta-d)(\cos\alpha+{\rm{i}}\sin\alpha)\\
=\cos(\theta+\alpha)+{\rm{i}}\sin(\theta+\alpha)+2d\sin\dfrac{\alpha}{2}\left(\sin\dfrac{\alpha}{2}-{\rm{i}}\cos\dfrac{\alpha}{2}\right)$，
因此 $M_1M_2$ 的方向复数为 $2d\sin\dfrac{\alpha}{2}\left(\sin\dfrac{\alpha}{2}-{\rm{i}}\cos\dfrac{\alpha}{2}\right)$，其垂直方向复数为 $n=2d\sin\dfrac{\alpha}{2}\left(
\cos\dfrac{\alpha}{2}+{\rm{i}}\sin\dfrac{\alpha}{2}\right)$．
又 $M_1M_2$ 中点位置 $M$ 为 $\cos(\theta+\alpha)+{\rm{i}}\sin(\theta+\alpha)+d\sin\dfrac{\alpha}{2}\left(\sin\dfrac{\alpha}{2}-{\rm{i}}\cos\dfrac{\alpha}{2}\right)$
设 $P$ 的位置 $x+y{\rm{i}}$，则 $\overrightarrow{MP}$ 代表的复数为 $z-[\cos(\theta+\alpha)+{\rm{i}}\sin(\theta+\alpha)+d\sin\dfrac{\alpha}{2}\left(\sin\dfrac{\alpha}{2}-{\rm{i}}\cos\dfrac{\alpha}{2}\right)]$
由题意知道，这个复数与 $n$ 共线，故 $\dfrac{y-\sin(\theta+\alpha)+d\sin\dfrac{\alpha}{2}\cos\dfrac{\alpha}{2}}{x-\cos(\theta+\alpha)-d\sin^2\dfrac{\alpha}{2}}=\tan\dfrac{
\alpha}{2}$
整理可得 $(y-\sin\theta)\cos\dfrac{\alpha}{2}+(d-\cos\theta-x)\sin\dfrac{\alpha}{2}=0$．
上式子关于 $\alpha$ 恒成立，则只能取 $x=d-\cos\theta$，$y=\sin\theta$．容易得到 $P$ 与 $A$ 关于两个圆的连心线的中垂线对称．
命题得证．
由题设知两动点具有相同角速度．
如图，$\odot O_1$ 和 $\odot O_2$ 上分别有两动点 $Q_1$ 和 $Q_2$．
则有 $\angle AO_1Q_1=\angle AO_2Q_2$（设为 $\theta$）．设两圆的另一个交点是 $B$，易知
$\angle ABQ_1=\dfrac{\theta}{2},\angle ABQ_2=180^\circ-\dfrac{\theta}{2}$，
于是 $\angle ABQ_1+\angle ABQ_2=180^\circ$，$Q_1,B,Q_2$ 共线．
过 $A$ 作 $MAN\perp AB$，其中 $M,N$ 分别在 $\odot O_1$ 和 $\odot O_2$ 上．于是 $\angle MQ_1Q_2=\angle NQ_2Q_1=90^\circ$，即四边形 $MQ_1Q_2N$ 为一直角梯形．这样 $Q_1Q_2$ 的中垂线过 $MN$ 中点，设其为 $P$．于是 $PQ_1=PQ_2$，$P$ 显然是所求之定点．
证法二
建立复平面，不妨设 $O_1$ 为原点，且圆 $O_1$ 半径为 $1$，$O_2$ 在实轴正半轴坐标为 $d$，设目前点转过的角度为 $\alpha$，$\alpha\in[0,2\pi)$，则点在圆 $O_1$ 位置 $M_1$ 为 $\cos(\theta+\alpha)+{\rm{i}\sin(\theta+\alpha)}$，点在圆 $O_2$ 的位置 $M_2$ 为 $d+(\cos\theta+{\rm{i}}\sin\theta-d)(\cos\alpha+{\rm{i}}\sin\alpha)\\
=\cos(\theta+\alpha)+{\rm{i}}\sin(\theta+\alpha)+2d\sin\dfrac{\alpha}{2}\left(\sin\dfrac{\alpha}{2}-{\rm{i}}\cos\dfrac{\alpha}{2}\right)$，
因此 $M_1M_2$ 的方向复数为 $2d\sin\dfrac{\alpha}{2}\left(\sin\dfrac{\alpha}{2}-{\rm{i}}\cos\dfrac{\alpha}{2}\right)$，其垂直方向复数为 $n=2d\sin\dfrac{\alpha}{2}\left(
\cos\dfrac{\alpha}{2}+{\rm{i}}\sin\dfrac{\alpha}{2}\right)$．
又 $M_1M_2$ 中点位置 $M$ 为 $\cos(\theta+\alpha)+{\rm{i}}\sin(\theta+\alpha)+d\sin\dfrac{\alpha}{2}\left(\sin\dfrac{\alpha}{2}-{\rm{i}}\cos\dfrac{\alpha}{2}\right)$
设 $P$ 的位置 $x+y{\rm{i}}$，则 $\overrightarrow{MP}$ 代表的复数为 $z-[\cos(\theta+\alpha)+{\rm{i}}\sin(\theta+\alpha)+d\sin\dfrac{\alpha}{2}\left(\sin\dfrac{\alpha}{2}-{\rm{i}}\cos\dfrac{\alpha}{2}\right)]$
由题意知道，这个复数与 $n$ 共线，故 $\dfrac{y-\sin(\theta+\alpha)+d\sin\dfrac{\alpha}{2}\cos\dfrac{\alpha}{2}}{x-\cos(\theta+\alpha)-d\sin^2\dfrac{\alpha}{2}}=\tan\dfrac{
\alpha}{2}$
整理可得 $(y-\sin\theta)\cos\dfrac{\alpha}{2}+(d-\cos\theta-x)\sin\dfrac{\alpha}{2}=0$．
上式子关于 $\alpha$ 恒成立，则只能取 $x=d-\cos\theta$，$y=\sin\theta$．容易得到 $P$ 与 $A$ 关于两个圆的连心线的中垂线对称．
命题得证．
答案
解析
备注
