已知平面 $\pi$ 上一点 $P$ 及 $\pi$ 外一点 $Q$．在 $\pi$ 上求一点 $R$，使得比值 $\dfrac{QP+PA}{QR}$ 为 最大．（美国）
【难度】
【出处】
1979年第21届IMO试题
【标注】
【答案】
略
【解析】
设 $Q$ 在 $\pi$ 上的射影为 $T$，$TP=a,QT=h$，$a,h$ 均是已知量．又设 $PR=x$，则
$\begin{aligned}
QP&=\sqrt[2]{h^2+a^2}\\
QR&=\sqrt[2]{QT^2+TR^2}\\
&\geqslant \sqrt[2]{h^2+(a-x)^2}
\end{aligned}$
于是 $\dfrac{QP+PR}{QR}\leqslant \dfrac{\sqrt{h^2+a^2}+x}{\sqrt{h^2+(a-x)^2}}$．
利用局部调整，在固定 $PR=x$ 的情况下，我们证明了 $R$ 一定在射线 $PT$ 上（$P,T$ 重合时另加讨论）．
如图，延长 $TP$ 至 $S$，使得 $QP=PS$，于是 $S$ 也是固定点．设 $\angle S=\dfrac{\theta}{2}$ 为固定角．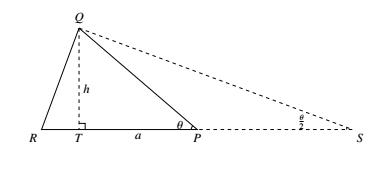
由正弦定理知 $\dfrac{QP+PR}{QR}=\dfrac{RS}{RQ}=\dfrac{\sin\angle RQS}{\sin\frac{\theta}{2}}\leqslant \dfrac{1}{\sin\frac{\theta}{2}}$．
等号取到，仅当 $\angle RQS=90^\circ$．
于是 $R$ 这样作．
（1）当 $P$ 与 $T$ 不重合时，设 $QP$ 与 $\pi$ 成 $\theta$ 角，$\theta$ 在 $\pi$ 上的射影为 $T$，$R$ 在 $PT$ 射线上，满足 $\angle QRP=90^\circ -\dfrac{\theta}{2}$．这时 $\dfrac{QP+PR}{QR}$ 达到最大值 $\dfrac{1}{\sin\frac{\theta}{2}}$．
（2）当 $P$ 与 $T$ 重合时，$R$ 是以 $P$ 为圆心，$QP$ 为半径的平面 $\pi$ 上的圆任何一点，此时最大值无疑为 $\dfrac{1}{\sin 45^\circ}=\sqrt{2}$．
$\begin{aligned}
QP&=\sqrt[2]{h^2+a^2}\\
QR&=\sqrt[2]{QT^2+TR^2}\\
&\geqslant \sqrt[2]{h^2+(a-x)^2}
\end{aligned}$
于是 $\dfrac{QP+PR}{QR}\leqslant \dfrac{\sqrt{h^2+a^2}+x}{\sqrt{h^2+(a-x)^2}}$．
利用局部调整，在固定 $PR=x$ 的情况下，我们证明了 $R$ 一定在射线 $PT$ 上（$P,T$ 重合时另加讨论）．
如图，延长 $TP$ 至 $S$，使得 $QP=PS$，于是 $S$ 也是固定点．设 $\angle S=\dfrac{\theta}{2}$ 为固定角．
由正弦定理知 $\dfrac{QP+PR}{QR}=\dfrac{RS}{RQ}=\dfrac{\sin\angle RQS}{\sin\frac{\theta}{2}}\leqslant \dfrac{1}{\sin\frac{\theta}{2}}$．等号取到，仅当 $\angle RQS=90^\circ$．
于是 $R$ 这样作．
（1）当 $P$ 与 $T$ 不重合时，设 $QP$ 与 $\pi$ 成 $\theta$ 角，$\theta$ 在 $\pi$ 上的射影为 $T$，$R$ 在 $PT$ 射线上，满足 $\angle QRP=90^\circ -\dfrac{\theta}{2}$．这时 $\dfrac{QP+PR}{QR}$ 达到最大值 $\dfrac{1}{\sin\frac{\theta}{2}}$．
（2）当 $P$ 与 $T$ 重合时，$R$ 是以 $P$ 为圆心，$QP$ 为半径的平面 $\pi$ 上的圆任何一点，此时最大值无疑为 $\dfrac{1}{\sin 45^\circ}=\sqrt{2}$．
答案
解析
备注
