在 $\triangle ABC$ 中，边 $AB=AC$．有一个圆内切于 $\triangle ABC$ 的外接圆，并且与 $AB、AC$ 分别相切于 $P、Q$．求证：$P,Q$ 两点联线的中点是 $\triangle ABC$ 的内切圆圆心．（美国）
【难度】
【出处】
1978年第20届IMO试题
【标注】
【答案】
略
【解析】
证法一
如图，设 $PQ$ 中点为 $I$，易知 $AI$ 已经平分 $\angle BAC$ 了，接下来只需证明 $CI$ 平分 $\angle ACB$ 即可．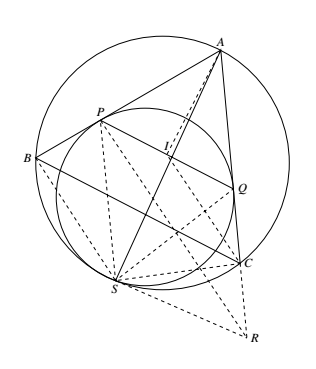
设两圆内切于 $S$，联结 $SB,SP,SA,SQ,SC$，易知 $SP$ 平分 $\angle ASB$，$SQ$ 平分 $\angle ASC$，故 $\dfrac{BS}{BP}=\dfrac{AS}{AP}=\dfrac{AS}{AQ}=\dfrac{SC}{CQ}$．①
延长 $QC$ 至 $R$，使 $QC=CR$，联结 $SR$．
于是由 ① 知 $\dfrac{BS}{BP}=\dfrac{SC}{CR}$
又 $\angle PBS=\angle SCR$
故 $\triangle PBS\sim\triangle SCR$．
于是 $\angle BPS=\angle CRS$，即 $A,R,S,P$ 共圆．
又 $IC$ 为 $\triangle PQR$ 之中位线，于是
$\begin{aligned}
\angle ACI&=\angle ARP=\angle ASP\\
&=\dfrac{1}{2}\angle ASB\\
&=\dfrac{1}{2}\angle ACB
\end{aligned}$
因此 $CI$ 平分 $\angle ACB$．
证法二
如图，设 $PQ$ 中点为 $I$，大圆圆心为 $O$，小圆圆心为 $T$，半径分别为 $R$ 和 $r$．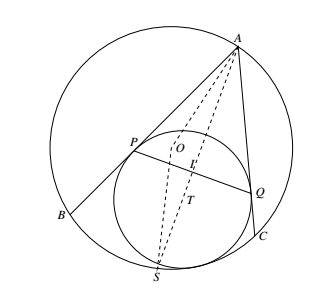
设 $AI$ 延长后交 $\odot O$ 于 $S$，则 $S$ 是 $\overparen{BSC}$ 中点，如能证明 $SI=BS=SC=2R\sin\dfrac{A}{2}$，则 $I$ 就是内心（这一熟知结论留给读者），下面我们证明 $SI=2R\sin\dfrac{A}{2}$．
联结 $SO,OA,OT$．
由相交弦定理及 $OT=R-r$ 知 $AT\cdot TS=(R+OT)(R-OT)=r(2R-r)$．
又 $AT=\dfrac{r}{\sin\frac{A}{2}},TS=AS-AT$
代入有 $\dfrac{1}{\sin\frac{A}{2}}\left(AS-\dfrac{r}{\sin\frac{A}{2}}\right)=2R-r$
此即 $AS-r\cot\dfrac{A}{2}\cos\dfrac{A}{2}=2R\sin\dfrac{A}{2}$
而易见 $r\cot\dfrac{A}{2}\cos\dfrac{A}{2}=AI$
于是 $SI=AS-AI=2R\sin\dfrac{A}{2}$．
如图，设 $PQ$ 中点为 $I$，易知 $AI$ 已经平分 $\angle BAC$ 了，接下来只需证明 $CI$ 平分 $\angle ACB$ 即可．
设两圆内切于 $S$，联结 $SB,SP,SA,SQ,SC$，易知 $SP$ 平分 $\angle ASB$，$SQ$ 平分 $\angle ASC$，故 $\dfrac{BS}{BP}=\dfrac{AS}{AP}=\dfrac{AS}{AQ}=\dfrac{SC}{CQ}$．①延长 $QC$ 至 $R$，使 $QC=CR$，联结 $SR$．
于是由 ① 知 $\dfrac{BS}{BP}=\dfrac{SC}{CR}$
又 $\angle PBS=\angle SCR$
故 $\triangle PBS\sim\triangle SCR$．
于是 $\angle BPS=\angle CRS$，即 $A,R,S,P$ 共圆．
又 $IC$ 为 $\triangle PQR$ 之中位线，于是
$\begin{aligned}
\angle ACI&=\angle ARP=\angle ASP\\
&=\dfrac{1}{2}\angle ASB\\
&=\dfrac{1}{2}\angle ACB
\end{aligned}$
因此 $CI$ 平分 $\angle ACB$．
证法二
如图，设 $PQ$ 中点为 $I$，大圆圆心为 $O$，小圆圆心为 $T$，半径分别为 $R$ 和 $r$．
设 $AI$ 延长后交 $\odot O$ 于 $S$，则 $S$ 是 $\overparen{BSC}$ 中点，如能证明 $SI=BS=SC=2R\sin\dfrac{A}{2}$，则 $I$ 就是内心（这一熟知结论留给读者），下面我们证明 $SI=2R\sin\dfrac{A}{2}$．联结 $SO,OA,OT$．
由相交弦定理及 $OT=R-r$ 知 $AT\cdot TS=(R+OT)(R-OT)=r(2R-r)$．
又 $AT=\dfrac{r}{\sin\frac{A}{2}},TS=AS-AT$
代入有 $\dfrac{1}{\sin\frac{A}{2}}\left(AS-\dfrac{r}{\sin\frac{A}{2}}\right)=2R-r$
此即 $AS-r\cot\dfrac{A}{2}\cos\dfrac{A}{2}=2R\sin\dfrac{A}{2}$
而易见 $r\cot\dfrac{A}{2}\cos\dfrac{A}{2}=AI$
于是 $SI=AS-AI=2R\sin\dfrac{A}{2}$．
答案
解析
备注
