在正方形 $ABCD$ 的内部作等边三角形 $ABK,BCL,CDM,DAN$．求证：四线段 $KL,LM,MN,NK$ 的中点和八线段 $AK,BK,BL,CL,CM,DM,DN,AN$ 的中点，是一个正十二边形的十二个顶点．（荷兰）
【难度】
【出处】
1977年第19届IMO试题
【标注】
【答案】
略
【解析】
如图，以正方形 $ABCD$ 的中心 $O$ 为原点，以正方形边长之半为长度单位建立直角坐标系，则正方形四个顶点的坐标分别为 $A(-1,-1),B(1,-1),C(1,1),D(-1,1)$．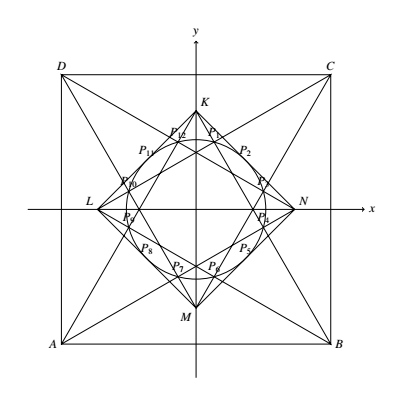
$K,L,M,N$ 四点坐标易知分别为 $K(0,\sqrt{3}-1),L(1-\sqrt{3},0),M(0,1-\sqrt{3}),N(\sqrt{3}-1,0)$．
$CL,NK,CM$ 的中点分别为 $P_1(1-\dfrac{\sqrt{3}}{2},\dfrac{1}{2}),P_2(\dfrac{\sqrt{3}-1}{2}),P_3(\dfrac{1}{2},1-\dfrac{\sqrt{3}}{2})$．
利用距离公式，得
$|OP_1|=|OP_2|=|OP_3|=\sqrt{2-\sqrt{3}}$．
$|P_1P_2|=|P_2P_3|=2-\sqrt{3}$．
由对称性可知，这十二条线段之中点，即图中的 $P_1,P_2,\cdots,P_{11},P_{12}$，均满足 $|OP_i|=\sqrt{2\sqrt{3}}(i=1,2,\cdots,12)$．$|P_iP_{i+1}|=2-\sqrt{3}(i=1,2,\cdots,12,P_{13}=P_1)$．因此，这十二个点是一个正十二边形的顶点．
$K,L,M,N$ 四点坐标易知分别为 $K(0,\sqrt{3}-1),L(1-\sqrt{3},0),M(0,1-\sqrt{3}),N(\sqrt{3}-1,0)$．$CL,NK,CM$ 的中点分别为 $P_1(1-\dfrac{\sqrt{3}}{2},\dfrac{1}{2}),P_2(\dfrac{\sqrt{3}-1}{2}),P_3(\dfrac{1}{2},1-\dfrac{\sqrt{3}}{2})$．
利用距离公式，得
$|OP_1|=|OP_2|=|OP_3|=\sqrt{2-\sqrt{3}}$．
$|P_1P_2|=|P_2P_3|=2-\sqrt{3}$．
由对称性可知，这十二条线段之中点，即图中的 $P_1,P_2,\cdots,P_{11},P_{12}$，均满足 $|OP_i|=\sqrt{2\sqrt{3}}(i=1,2,\cdots,12)$．$|P_iP_{i+1}|=2-\sqrt{3}(i=1,2,\cdots,12,P_{13}=P_1)$．因此，这十二个点是一个正十二边形的顶点．
答案
解析
备注
