设 $A$ 是平面直角坐标系上三条直线 $x=1$，$y=0$ 和 $y=t(2x-t)$ 围成的闭区域，其中 $0<t<1$．证明：在区域 $A$ 内，以 $P(t,t^2)$，$Q(1,0)$ 为其中两个顶点的三角形的面积不超过 $\dfrac{1}{4}$．
【难度】
【出处】
2013第12届CGMO试题
【标注】
【答案】
略
【解析】
易知这三条直线围成的闭区域是一个三角形的内部与边界，此三角形的三个顶点分别为 $B(\frac{t}{2},0)$，$Q(1,0)$，$C(1,t(2-t))$．在三角形 $BQC$ 内任取一点 $X$，则三角形 $PQX$ 的面积等于 $PQ$ 乘以 $X$ 到 $PQ$ 距离的一半，故当 $X$ 到 $PQ$ 距离最大，即 $X$ 取到 $B$ 点或 $C$ 点时，三角形 $PQX$ 的面积最大．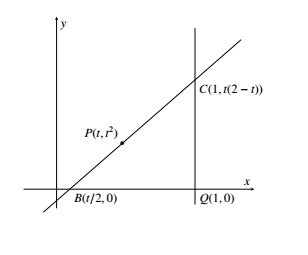
三角形 $PQB$ 的面积为
$\begin{aligned}
\frac{1}{2}\left(1-\frac{t^2}{2}\right)t^2 &=\frac{1}{4}(2-t)t^2 \leqslant \frac{1}{4}(2-t)t\\
&\leqslant \frac{1}{4}\left(\frac{2-t+t}{2}\right)^2 =\frac{1}{4}
\end{aligned}$
三角形 $PQC$ 的面积为
$\begin{aligned}
\frac{1}{2}(1-t)(2t-t^2) &=\frac{1}{4}2t(1-t)(2-t)\\
&\leqslant \frac{1}{4}\left(\frac{2t+1-t+2-t}{3}\right)^3 =\frac{1}{4}
\end{aligned}$
因此在区域 $A$ 内，以 $P,Q$ 为其中两个顶点的三角形的面积不超过 $\frac{1}{4}$，证毕．
三角形 $PQB$ 的面积为$\begin{aligned}
\frac{1}{2}\left(1-\frac{t^2}{2}\right)t^2 &=\frac{1}{4}(2-t)t^2 \leqslant \frac{1}{4}(2-t)t\\
&\leqslant \frac{1}{4}\left(\frac{2-t+t}{2}\right)^2 =\frac{1}{4}
\end{aligned}$
三角形 $PQC$ 的面积为
$\begin{aligned}
\frac{1}{2}(1-t)(2t-t^2) &=\frac{1}{4}2t(1-t)(2-t)\\
&\leqslant \frac{1}{4}\left(\frac{2t+1-t+2-t}{3}\right)^3 =\frac{1}{4}
\end{aligned}$
因此在区域 $A$ 内，以 $P,Q$ 为其中两个顶点的三角形的面积不超过 $\frac{1}{4}$，证毕．
答案
解析
备注
