如图，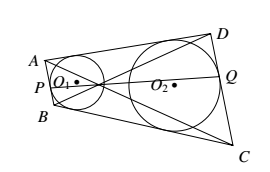
在梯形ABCD中，$AB\parallel CD$，$\odot O_1$ 与 $DA,AB,BC$ 三边相切，
$\odot O_2$ 与 $BC,CD,DA$ 三边相切．设 $P$ 是 $\odot O_1$ 与边 $AB$ 的切点，$Q$ 是 $\odot O_2$ 与边 $CD$ 的切点．证明：$AC,BD,PQ$ 三线共点．
在梯形ABCD中，$AB\parallel CD$，$\odot O_1$ 与 $DA,AB,BC$ 三边相切，$\odot O_2$ 与 $BC,CD,DA$ 三边相切．设 $P$ 是 $\odot O_1$ 与边 $AB$ 的切点，$Q$ 是 $\odot O_2$ 与边 $CD$ 的切点．证明：$AC,BD,PQ$ 三线共点．
【难度】
【出处】
2013第12届CGMO试题
【标注】
【答案】
略
【解析】
设直线 $AC,BD$ 的交点为 $R$，连结 $O_1 A,O_1 B,O_1 P,O_2 C,O_2 D,O_2 Q,PR,QR$．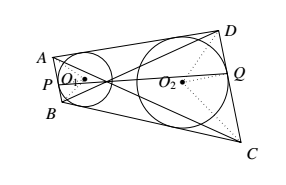
由于 $BA,BC$ 是 $\odot O_1$ 的切线，故 $\angle PBO_1 =\angle CBO_1 ,\frac{1}{2}\angle ABC$，同理 $\angle QCO_2 =\frac{1}{2}\angle BCD$．
由 $AB\parallel CD$ 知 $\angle ABC+\angle BCD=180^{\circ}$，因此 $\angle PBO_1 +\angle QCO_2 =90^{\circ}$，故 $\text{Rt}\triangle O_1 BP$ 与 $\text{Rt}\triangle CO_2 Q$ 相似，我们有 $
\frac{O_{1} P}{B P}=\frac{C Q}{O_{2} Q}
$．
同理有 $\frac{A P}{O_{1} P}=\frac{O_{2} Q}{D Q}$，两式相乘得 $\frac{A P}{B P}=\frac{C Q}{D Q}$．
再由等比定理知 $\frac{A P}{A P+B P}=\frac{C Q}{C Q+D Q}$，即 $\frac{A P}{A B}=\frac{C Q}{C D}$．
由 $AB\parallel CD$ 知 $\triangle ABR$ 与 $\triangle CDR$ 相似，故 $\frac{A R}{A B}=\frac{C R}{C D}$．
再与 $\frac{A P}{A B}=\frac{C Q}{C D}$ 比较得 $\frac{A R}{A P}=\frac{C R}{C Q}$．
又由于 $\angle PAR=\angle QCR$，故 $\triangle PAR$ 与 $\triangle QCR$ 相似，因此 $\angle PRA=\angle QRC$．
所以 $P,R,Q$ 三点共线，即 $AC,BD,PQ$ 三线共点，证毕．
由于 $BA,BC$ 是 $\odot O_1$ 的切线，故 $\angle PBO_1 =\angle CBO_1 ,\frac{1}{2}\angle ABC$，同理 $\angle QCO_2 =\frac{1}{2}\angle BCD$．由 $AB\parallel CD$ 知 $\angle ABC+\angle BCD=180^{\circ}$，因此 $\angle PBO_1 +\angle QCO_2 =90^{\circ}$，故 $\text{Rt}\triangle O_1 BP$ 与 $\text{Rt}\triangle CO_2 Q$ 相似，我们有 $
\frac{O_{1} P}{B P}=\frac{C Q}{O_{2} Q}
$．
同理有 $\frac{A P}{O_{1} P}=\frac{O_{2} Q}{D Q}$，两式相乘得 $\frac{A P}{B P}=\frac{C Q}{D Q}$．
再由等比定理知 $\frac{A P}{A P+B P}=\frac{C Q}{C Q+D Q}$，即 $\frac{A P}{A B}=\frac{C Q}{C D}$．
由 $AB\parallel CD$ 知 $\triangle ABR$ 与 $\triangle CDR$ 相似，故 $\frac{A R}{A B}=\frac{C R}{C D}$．
再与 $\frac{A P}{A B}=\frac{C Q}{C D}$ 比较得 $\frac{A R}{A P}=\frac{C R}{C Q}$．
又由于 $\angle PAR=\angle QCR$，故 $\triangle PAR$ 与 $\triangle QCR$ 相似，因此 $\angle PRA=\angle QRC$．
所以 $P,R,Q$ 三点共线，即 $AC,BD,PQ$ 三线共点，证毕．
答案
解析
备注
