如图所示，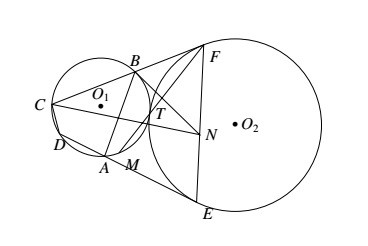
$\odot O_1$ 与 $\odot O_2$ 外切于点 $T$，四边形 $ABCD$ 内接于 $\odot O_1$，直线 $DA,CB$ 分别切 $\odot O_2$ 于点 $E,F$．直线 $BN$ 平分 $\angle ABF$ 并与线段 $EF$ 交于点 $N$．直线 $FT$ 交 $\overparen{AT}$（不包含点 $B$ 的弧）内于点 $M$．求证：点 $M$ 为 $\triangle BCN$ 的外心．
$\odot O_1$ 与 $\odot O_2$ 外切于点 $T$，四边形 $ABCD$ 内接于 $\odot O_1$，直线 $DA,CB$ 分别切 $\odot O_2$ 于点 $E,F$．直线 $BN$ 平分 $\angle ABF$ 并与线段 $EF$ 交于点 $N$．直线 $FT$ 交 $\overparen{AT}$（不包含点 $B$ 的弧）内于点 $M$．求证：点 $M$ 为 $\triangle BCN$ 的外心．【难度】
【出处】
2013第12届CGMO试题
【标注】
【答案】
略
【解析】
设 $AM$ 的延长线交 $EF$ 于点 $P$．连结 $AT, BM, BP, BT, CM, CT, ET, TP$．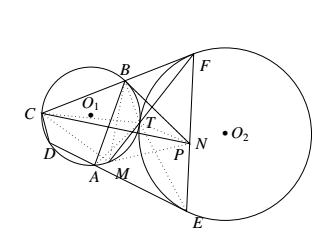
由 $BF$ 与 $\odot O_2$ 相切于 $F$ 点，可得 $\angle BFT=\angle FET$．
由 $\odot O_1$ 与 $\odot O_2$ 外切于点 $T$，可得 $\angle MBT=\angle FET$．因此 $\angle MBT=\angle BFM$．于是 $\triangle MBT$ 与 $\triangle MFB$ 相似，从而 $MB^2 = MT\cdot MF$．同理可得 $MC^2 =MT\cdot MF$．
又由 $\odot O_1$ 与 $\odot O_2$ 外切于点 $T$，可得 $\angle MAT=\angle FET$．因此 $A, E, P, T$ 四点共圆，从而 $\angle APT=\angle AET$．由 $AE$ 与 $\odot O_2$ 相切于 $E$ 点，可得 $\angle AET=\angle EFT$．因此 $\angle MPT=\angle PFM$．于是 $\triangle MPT$ 与 $\triangle MFP$ 相似，从而 $MP^2 =MT\cdot MF$．
由前面可得 $MC=MB=MP$．从而点 $M$ 是 $\triangle BCP$ 外接圆的圆心．于是 $\angle FBP=\frac{1}{2}\angle CMP$．$\angle CMP=\angle CDA=\angle ABF$．由题意得 $\angle FBN=\frac{1}{2}\angle ABF$．从而 $\angle FBN=\angle FBP$，即点 $P$ 与 $N$ 重合．证毕．
由 $BF$ 与 $\odot O_2$ 相切于 $F$ 点，可得 $\angle BFT=\angle FET$．由 $\odot O_1$ 与 $\odot O_2$ 外切于点 $T$，可得 $\angle MBT=\angle FET$．因此 $\angle MBT=\angle BFM$．于是 $\triangle MBT$ 与 $\triangle MFB$ 相似，从而 $MB^2 = MT\cdot MF$．同理可得 $MC^2 =MT\cdot MF$．
又由 $\odot O_1$ 与 $\odot O_2$ 外切于点 $T$，可得 $\angle MAT=\angle FET$．因此 $A, E, P, T$ 四点共圆，从而 $\angle APT=\angle AET$．由 $AE$ 与 $\odot O_2$ 相切于 $E$ 点，可得 $\angle AET=\angle EFT$．因此 $\angle MPT=\angle PFM$．于是 $\triangle MPT$ 与 $\triangle MFP$ 相似，从而 $MP^2 =MT\cdot MF$．
由前面可得 $MC=MB=MP$．从而点 $M$ 是 $\triangle BCP$ 外接圆的圆心．于是 $\angle FBP=\frac{1}{2}\angle CMP$．$\angle CMP=\angle CDA=\angle ABF$．由题意得 $\angle FBN=\frac{1}{2}\angle ABF$．从而 $\angle FBN=\angle FBP$，即点 $P$ 与 $N$ 重合．证毕．
答案
解析
备注
