在任意 $\triangle ABC$ 的边上向外作 $\triangle ABR,\triangle BCP,\triangle CAQ$，使得 $\angle CBP=\angle CAQ=45^\circ$，$\angle BCP=\angle ACQ=30^\circ$，$\angle ABR=\angle BAR=15^\circ$．试证：$\angle QRP=90^\circ;QR=RP$．（荷兰）
【难度】
【出处】
1975年第17届IMO试题
【标注】
【答案】
略
【解析】
证法一
如图所示．先讨论 $A,C$ 在 $QR$ 同侧，$C,R$ 在 $PR$ 异侧的情况，如有同侧，则同理可证．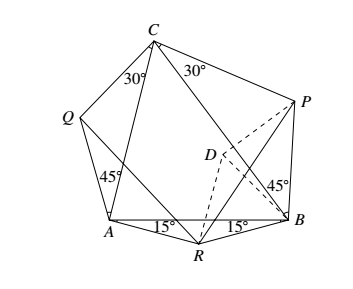
由于 $\angle QRA+\angle AQR=120^\circ -\angle CAB$
$\angle PRB+\angle BPQ=120^\circ -\angle CBA$
于是
$\angle QRA+\angle AQR+\angle PRB+\angle BPR=240^\circ-\angle CAB-\angle CBA=60^\circ+\angle ACB$．
毫无疑问，$\min(\angle QRA,\angle PRB)<60^\circ$ 和 $\min(\angle AQR,\angle BPR)<\angle ACB$ 至少有一个成立．为方便起见，不妨设
$\angle PRB<60^\circ$ 或 $\angle BPR<\angle ACB$．
今以 $RB$ 为边向内作正三角形 $\triangle DRB$，联结 $PD$．
易知 $\angle PBD=\angle PBR-60^\circ=\angle CBA$．
又 $\dfrac{PB}{BC}=\dfrac{\sin 30^\circ}{\sin 75^\circ}=\dfrac{1}{2\cos 15^\circ}$，
而 $\dfrac{BD}{AB}=\dfrac{BR}{AB}=\dfrac{1}{2\cos 15^\circ}$．
因此 $\dfrac{PB}{BC}=\dfrac{BD}{AB}$．
于是 $\triangle BPD\sim\triangle BCA$．
由 ① 及 $\angle DRB=60^\circ$ 和 $\angle DPB=\angle ACB$ 知 $B,D$ 在 $RP$ 之异侧．
又
$\begin{aligned}
\angle PDR&=60^\circ+\angle PDB\\
&=60^\circ+\angle CAB\\
&=\angle QAR
\end{aligned}$
$DR=AR$．又由于 $\triangle CQA\sim\triangle CPB$，知 $\dfrac{DP}{AC}=\dfrac{BP}{BC}=\dfrac{AQ}{AC}$，
故 $DP=AQ$．
于是 $\triangle QAR\cong\triangle PDR(SAS)$．
便有 $QR=RP$．
另外还有
$\begin{aligned}
\angle QRP&=\angle QRD+\angle DRP\\
&=\angle QRD+\angle ARQ\\
&=\angle DRA\\
&=150^\circ-60^\circ\\
&=90^\circ
\end{aligned}$
证法二
此题可用复数方法快速解决．
建立一个复平面，如图，令 $A=-1,B=1,R,P,Q,C$ 都表示复数．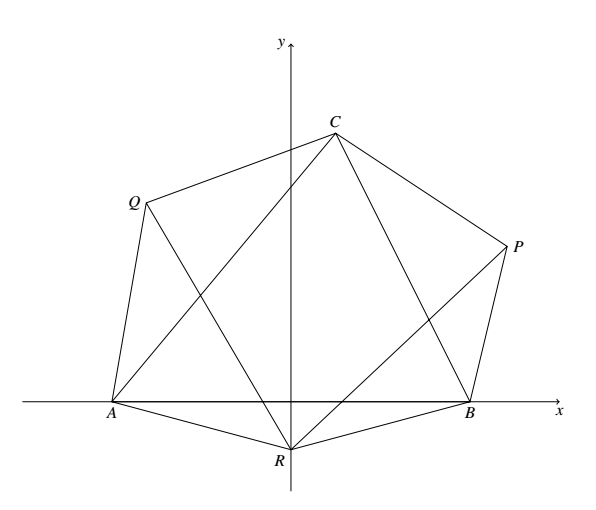
易知，$R=-i\tan 15^\circ$．
又 $\dfrac{P-B}{C-B}=\dfrac{|BP|}{|BC|}(\cos 45^\circ-i\sin 45^\circ)$，
即 $\dfrac{P-1}{C-1}=\dfrac{\sin 30^\circ}{\sin 75^\circ}(\cos 45^\circ-i\sin 45^\circ)$，
得 $P=\dfrac{C-1}{4\cos 15^\circ}(\sqrt{2}-\sqrt{2}i)+1$
同理 $Q=\dfrac{C+1}{4\cos 15^\circ}(\sqrt{2}+\sqrt{2}i)-1$
$\begin{aligned}
Q-iP&=\dfrac{\sqrt{2}+\sqrt{2}i}{2\cos 15^\circ}-1-i\\
&(1+i)\left(\dfrac{\sqrt{2}}{2\cos 15^\circ}-1\right)\\
&=-(1+i)\tan 15^\circ\\
&=(1-i)R
\end{aligned}$
此即 $Q-R=i(P-R)$．
因此 $\triangle QRP$ 为一等腰直角三角形．
如图所示．先讨论 $A,C$ 在 $QR$ 同侧，$C,R$ 在 $PR$ 异侧的情况，如有同侧，则同理可证．
由于 $\angle QRA+\angle AQR=120^\circ -\angle CAB$$\angle PRB+\angle BPQ=120^\circ -\angle CBA$
于是
$\angle QRA+\angle AQR+\angle PRB+\angle BPR=240^\circ-\angle CAB-\angle CBA=60^\circ+\angle ACB$．
毫无疑问，$\min(\angle QRA,\angle PRB)<60^\circ$ 和 $\min(\angle AQR,\angle BPR)<\angle ACB$ 至少有一个成立．为方便起见，不妨设
$\angle PRB<60^\circ$ 或 $\angle BPR<\angle ACB$．
今以 $RB$ 为边向内作正三角形 $\triangle DRB$，联结 $PD$．
易知 $\angle PBD=\angle PBR-60^\circ=\angle CBA$．
又 $\dfrac{PB}{BC}=\dfrac{\sin 30^\circ}{\sin 75^\circ}=\dfrac{1}{2\cos 15^\circ}$，
而 $\dfrac{BD}{AB}=\dfrac{BR}{AB}=\dfrac{1}{2\cos 15^\circ}$．
因此 $\dfrac{PB}{BC}=\dfrac{BD}{AB}$．
于是 $\triangle BPD\sim\triangle BCA$．
由 ① 及 $\angle DRB=60^\circ$ 和 $\angle DPB=\angle ACB$ 知 $B,D$ 在 $RP$ 之异侧．
又
$\begin{aligned}
\angle PDR&=60^\circ+\angle PDB\\
&=60^\circ+\angle CAB\\
&=\angle QAR
\end{aligned}$
$DR=AR$．又由于 $\triangle CQA\sim\triangle CPB$，知 $\dfrac{DP}{AC}=\dfrac{BP}{BC}=\dfrac{AQ}{AC}$，
故 $DP=AQ$．
于是 $\triangle QAR\cong\triangle PDR(SAS)$．
便有 $QR=RP$．
另外还有
$\begin{aligned}
\angle QRP&=\angle QRD+\angle DRP\\
&=\angle QRD+\angle ARQ\\
&=\angle DRA\\
&=150^\circ-60^\circ\\
&=90^\circ
\end{aligned}$
证法二
此题可用复数方法快速解决．
建立一个复平面，如图，令 $A=-1,B=1,R,P,Q,C$ 都表示复数．
易知，$R=-i\tan 15^\circ$．又 $\dfrac{P-B}{C-B}=\dfrac{|BP|}{|BC|}(\cos 45^\circ-i\sin 45^\circ)$，
即 $\dfrac{P-1}{C-1}=\dfrac{\sin 30^\circ}{\sin 75^\circ}(\cos 45^\circ-i\sin 45^\circ)$，
得 $P=\dfrac{C-1}{4\cos 15^\circ}(\sqrt{2}-\sqrt{2}i)+1$
同理 $Q=\dfrac{C+1}{4\cos 15^\circ}(\sqrt{2}+\sqrt{2}i)-1$
$\begin{aligned}
Q-iP&=\dfrac{\sqrt{2}+\sqrt{2}i}{2\cos 15^\circ}-1-i\\
&(1+i)\left(\dfrac{\sqrt{2}}{2\cos 15^\circ}-1\right)\\
&=-(1+i)\tan 15^\circ\\
&=(1-i)R
\end{aligned}$
此即 $Q-R=i(P-R)$．
因此 $\triangle QRP$ 为一等腰直角三角形．
答案
解析
备注
