把一块 $8×8$ 的国际象棋棋盘分割成 $p$ 个矩形,分割时不能割破棋盘的任何一格(即只能沿棋盘的分割线割开),并且还要满足下面两个条件:
(1)每个矩形中含有同样多的黑格和白格;
(2)如果第 $i$ 个矩形中白格数为 ${a}_{i}$,那么有 ${a}_{1}<{a}_{2}<\cdots<{a}_{p}$.
试在所有可能分法中,求出 $p$ 的最大值,并且对这个最大值 $p$ 列出所有可能的数列 ${a}_{1},{a}_{2},\cdots,{a}_{p}$.(保加利亚)
(1)每个矩形中含有同样多的黑格和白格;
(2)如果第 $i$ 个矩形中白格数为 ${a}_{i}$,那么有 ${a}_{1}<{a}_{2}<\cdots<{a}_{p}$.
试在所有可能分法中,求出 $p$ 的最大值,并且对这个最大值 $p$ 列出所有可能的数列 ${a}_{1},{a}_{2},\cdots,{a}_{p}$.(保加利亚)
【难度】
【出处】
1974年第16届IMO试题
【标注】
【答案】
略
【解析】
因为棋盘有 $32$ 个白方格,所以 $a_1+a_2+\cdots+a_p=32$.
由(2),$a_1\geqslant 1,a_2\geqslant 2,\cdots,a_p\geqslant p$,所以 $1+2+\cdots+p\leqslant 32$,$p^2+p\leqslant 64$,故 $p\leqslant 7$.即至多分割成 $7$ 个满足题意的矩形.
当 $p=7$ 时,有如下五种可能的组合:\begin{array} &&a_1 & a_2 & a_3&a_4&a_5&a_6&a_7 \\(1)&1&2&3&4&5&6&11\\(2)&1&2&3&4&5&7&10\\(3)&1&2&3&4&5&8&9\\(4)&1&2&3&4&6&7&9\\(5)&1&2&3&5&6&7&8\end{array}第一种组合是不可能在棋盘上实现的,因为棋盘上不可能分割出 $22$ 格的矩形.所有其他的情况都是可能的,具体的分法如下图所示(图中的数字表示该块含方格数).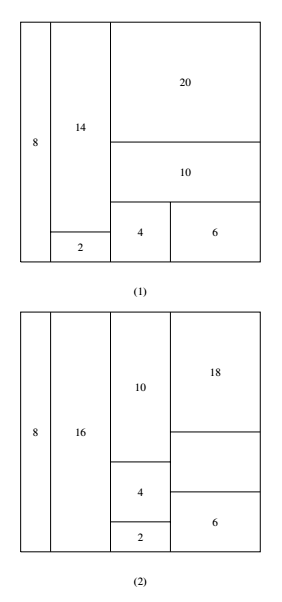

由(2),$a_1\geqslant 1,a_2\geqslant 2,\cdots,a_p\geqslant p$,所以 $1+2+\cdots+p\leqslant 32$,$p^2+p\leqslant 64$,故 $p\leqslant 7$.即至多分割成 $7$ 个满足题意的矩形.
当 $p=7$ 时,有如下五种可能的组合:\begin{array} &&a_1 & a_2 & a_3&a_4&a_5&a_6&a_7 \\(1)&1&2&3&4&5&6&11\\(2)&1&2&3&4&5&7&10\\(3)&1&2&3&4&5&8&9\\(4)&1&2&3&4&6&7&9\\(5)&1&2&3&5&6&7&8\end{array}第一种组合是不可能在棋盘上实现的,因为棋盘上不可能分割出 $22$ 格的矩形.所有其他的情况都是可能的,具体的分法如下图所示(图中的数字表示该块含方格数).


答案
解析
备注