设 $\triangle ABC$ 的三个内角分别是 $\angle A=\alpha,\angle B=\beta,\angle C=\gamma$．试证在 $AB$ 上有一点 $D$，使 $CD$ 为 $AD$ 和 $BD$ 的几何中项的充要条件是 $\sin \alpha\sin \beta\leqslant {{\sin }^{2}}\dfrac{\gamma}{2}$．（芬兰）
【难度】
【出处】
1974年第16届IMO试题
【标注】
【答案】
略
【解析】
证法一
如图，作 $\triangle ABC$ 外接圆，延长 $CD$ 交圆于 $M$，则有相交弦定理 $CD\cdot MD=AD\cdot BD$．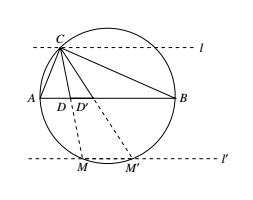
又如同时有条件 $CD^2=AD\cdot BD$，则必有 $CD=MD$，即 $D$ 为 $CM$ 中点．
今过 $C,M$ 分别作直线 $l,l^\prime$ 与 $AB$ 平行，则易知 $l,l^\prime$ 关于 $AB$ 对称．$D$ 存在的充要条件就是 $l^\prime$ 与外接圆有交点．
设 $\overparen{MM^\prime}$ 中点为 $P$，则上述充要条件变为：$P$ 至 $AB$ 法人距离 $\geqslant C$ 至 $AB$ 的距离，这一条件还可以转化为：$S_{\triangle ABP}\geqslant S_{\triangle ABC}$，
记外接圆半径为 $R$，则 $S_{\triangle ABC}=\dfrac{1}{2}AC\cdot BC\cdot \sin C=2R^2\sin\alpha \sin\beta\sin\gamma$．
又 $\angle APB=180^\circ-\angle C=180^\circ-\gamma$．
$AP=BP=2R\sin\dfrac{\gamma}{2}$．
故 $S_{\triangle ABP}=\dfrac{1}{2}AP\cdot BP\cdot \sin\angle APB=2R^2\sin^2\dfrac{\gamma}{2}\sin\gamma$．
于是 ① 就化为 $\sin\alpha\sin\beta\leqslant\sin^2\dfrac{\gamma}{2}$．
注意等式成立当且仅当 $l^\prime$ 与外接圆相切，这时在 $AB$ 上只有一点 $D$ 使 $CD^2=AD\cdot BD.$
证法二
如图，设 $\angle ACD=\gamma_1,\angle BCD=\gamma_2$．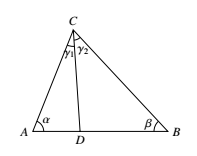
由正弦定理 $\dfrac{CD}{AD}=\dfrac{\sin\alpha}{\sin\gamma_1},\dfrac{CD}{BD}=\dfrac{\sin\beta}{\sin\gamma_2}$．
于是 $CD^2=AD\cdot BD$ 等价于 $\sin\gamma_1\sin\gamma_2=\sin\alpha\sin\beta$．
记 $f(x)=\sin x\sin(\gamma-x),0<x<\gamma$．
则利用积化和差，可得
$\begin{aligned}
f(x)&=\dfrac{1}{2}\cos(2x-\gamma)-\dfrac{1}{2}\cos\gamma\\
&\leqslant \dfrac{1}{2}(1-\cos\gamma)\\
&=\sin^\dfrac{\gamma}{2}
\end{aligned}$
此即 $\sin\alpha\sin\beta\leqslant \sin^2\dfrac{\gamma}{2}$．②
又由 $-\gamma<2x-\gamma<\gamma$ 及余弦函数的连续性知 $f(x)$ 的值域为 $(0,\sin^2\dfrac{\gamma}{2})$．只要 ② 满足，必存在 $x\in(0,\gamma)$，（而且由余弦函数是偶函数，一般情况下还有两个解）满足：$\sin x\sin(\gamma-x)=\sin\alpha\sin\beta$．
令 $x=\gamma_1,\gamma-x=\gamma_2$，即得 $D$ 的位置．
当 $\sin\alpha\sin\beta=\sin^2\dfrac{\gamma}{2}$ 时，只能有 $\cos(2x-\gamma)=1$，只能有 $x=\dfrac{\gamma}{2}=\gamma_1=\gamma_2$，此时 $D$ 只有一个，$AD$ 是 $\angle A$ 的平分线．
如图，作 $\triangle ABC$ 外接圆，延长 $CD$ 交圆于 $M$，则有相交弦定理 $CD\cdot MD=AD\cdot BD$．
又如同时有条件 $CD^2=AD\cdot BD$，则必有 $CD=MD$，即 $D$ 为 $CM$ 中点．今过 $C,M$ 分别作直线 $l,l^\prime$ 与 $AB$ 平行，则易知 $l,l^\prime$ 关于 $AB$ 对称．$D$ 存在的充要条件就是 $l^\prime$ 与外接圆有交点．
设 $\overparen{MM^\prime}$ 中点为 $P$，则上述充要条件变为：$P$ 至 $AB$ 法人距离 $\geqslant C$ 至 $AB$ 的距离，这一条件还可以转化为：$S_{\triangle ABP}\geqslant S_{\triangle ABC}$，
记外接圆半径为 $R$，则 $S_{\triangle ABC}=\dfrac{1}{2}AC\cdot BC\cdot \sin C=2R^2\sin\alpha \sin\beta\sin\gamma$．
又 $\angle APB=180^\circ-\angle C=180^\circ-\gamma$．
$AP=BP=2R\sin\dfrac{\gamma}{2}$．
故 $S_{\triangle ABP}=\dfrac{1}{2}AP\cdot BP\cdot \sin\angle APB=2R^2\sin^2\dfrac{\gamma}{2}\sin\gamma$．
于是 ① 就化为 $\sin\alpha\sin\beta\leqslant\sin^2\dfrac{\gamma}{2}$．
注意等式成立当且仅当 $l^\prime$ 与外接圆相切，这时在 $AB$ 上只有一点 $D$ 使 $CD^2=AD\cdot BD.$
证法二
如图，设 $\angle ACD=\gamma_1,\angle BCD=\gamma_2$．
由正弦定理 $\dfrac{CD}{AD}=\dfrac{\sin\alpha}{\sin\gamma_1},\dfrac{CD}{BD}=\dfrac{\sin\beta}{\sin\gamma_2}$．于是 $CD^2=AD\cdot BD$ 等价于 $\sin\gamma_1\sin\gamma_2=\sin\alpha\sin\beta$．
记 $f(x)=\sin x\sin(\gamma-x),0<x<\gamma$．
则利用积化和差，可得
$\begin{aligned}
f(x)&=\dfrac{1}{2}\cos(2x-\gamma)-\dfrac{1}{2}\cos\gamma\\
&\leqslant \dfrac{1}{2}(1-\cos\gamma)\\
&=\sin^\dfrac{\gamma}{2}
\end{aligned}$
此即 $\sin\alpha\sin\beta\leqslant \sin^2\dfrac{\gamma}{2}$．②
又由 $-\gamma<2x-\gamma<\gamma$ 及余弦函数的连续性知 $f(x)$ 的值域为 $(0,\sin^2\dfrac{\gamma}{2})$．只要 ② 满足，必存在 $x\in(0,\gamma)$，（而且由余弦函数是偶函数，一般情况下还有两个解）满足：$\sin x\sin(\gamma-x)=\sin\alpha\sin\beta$．
令 $x=\gamma_1,\gamma-x=\gamma_2$，即得 $D$ 的位置．
当 $\sin\alpha\sin\beta=\sin^2\dfrac{\gamma}{2}$ 时，只能有 $\cos(2x-\gamma)=1$，只能有 $x=\dfrac{\gamma}{2}=\gamma_1=\gamma_2$，此时 $D$ 只有一个，$AD$ 是 $\angle A$ 的平分线．
答案
解析
备注
