$O$ 是直线 $g$ 上的一点，$\overrightarrow{O{{P}_{1}}},\overrightarrow{O{{P}_{2}}},...,\overrightarrow{O{{P}_{n}}}$ 都是单位长度的向量，其中所有点 $P_i$ 都在通过 $g$ 的同一平面上，且在 $g$ 的同侧．求证：若 $n$ 为奇数，则有 $\left| \overrightarrow{O{{P}_{1}}}+\overrightarrow{O{{P}_{2}}}+...+\overrightarrow{O{{P}_{n}}} \right|\geqslant 1$，这里 $\left| \overrightarrow{OM} \right|$ 表示向量 $\overrightarrow{OM}$ 的长度．（捷克斯洛伐克）
【难度】
【出处】
1973年第15届IMO试题
【标注】
【答案】
略
【解析】
易知，若向量 $\overrightarrow{u}$ 和 $\overrightarrow{w}$ 之间的夹角 $\leqslant\dfrac{\pi}{2}$，则 $|\overrightarrow{u}+\overrightarrow{w}|\geqslant \max\{\overrightarrow{u},\overrightarrow{w}\}$．
因为 $n=2k-1$ 为奇数，下面对正整数 $k$ 用数学归纳法．不妨设 $P_i$ 是使得它们沿中心 $O$ 的半圆随着递增下标依次以逆时针方向排列，用 $\overrightarrow{u_i}$ 表示 $\overrightarrow{OP_i}$，并用 $\overrightarrow{u}$ 表示 $\displaystyle \sum\limits_{i=1}^n\overrightarrow{u_i}$．
当 $k=1$ 时，$n=1$，此时 $|\overrightarrow{u}|=|\overrightarrow{u_1}|=1$，命题成立．
假设命题对小于 $k$ 的正整数成立．对于正整数 $k$，记 $\displaystyle \overrightarrow{v}=\sum\limits_{i=2}^{2k}\overrightarrow{u_i}$，则由归纳假设，$|\overrightarrow{v}|\geqslant 1$，且 $\overrightarrow{v}$ 在 $\overrightarrow{u_2}$ 与 $\overrightarrow{u_{2k}}$ 之间，即在 $\angle P_{2k+1}OP_1$ 内．
设 $\overrightarrow{w}=\overrightarrow{u_1}+\overrightarrow{u_{2k+1}}$，则 $\displaystyle \overrightarrow{u}=\overrightarrow{v}+\overrightarrow{w}=\sum\limits_{i=1}^{2k+1}\overrightarrow{u_i}$．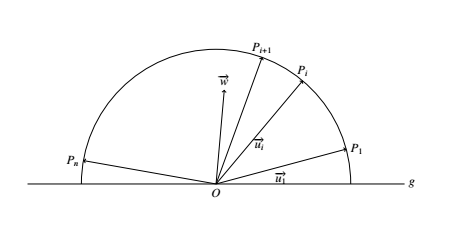
当 $\overrightarrow{w}=\overrightarrow{0}$ 时，有 $|\overrightarrow{u}|=|\overrightarrow{v}|\geqslant 1$；
当 $\overrightarrow{w}\ne\overrightarrow{0}$ 时，向量 $\overrightarrow{w}$ 平分角 $\angle P_1OP_{2k+1}$，因此 $\overrightarrow{w}$ 与 $\overrightarrow{u_1}$ 和 $\overrightarrow{u_{2k+1}}$ 的夹角小于 $\dfrac{\pi}{2}$，从而 $\overrightarrow{w}$ 与 $\overrightarrow{v}$ 的夹角小于 $\dfrac{\pi}{2}$，于是 $|\overrightarrow{u}|=|\overrightarrow{v}+\overrightarrow{w}|\geqslant |\overrightarrow{v}|\geqslant 1$，即命题对 $k$ 也成立．
从而命题对一切正奇数 $n$ 都成立．
因为 $n=2k-1$ 为奇数，下面对正整数 $k$ 用数学归纳法．不妨设 $P_i$ 是使得它们沿中心 $O$ 的半圆随着递增下标依次以逆时针方向排列，用 $\overrightarrow{u_i}$ 表示 $\overrightarrow{OP_i}$，并用 $\overrightarrow{u}$ 表示 $\displaystyle \sum\limits_{i=1}^n\overrightarrow{u_i}$．
当 $k=1$ 时，$n=1$，此时 $|\overrightarrow{u}|=|\overrightarrow{u_1}|=1$，命题成立．
假设命题对小于 $k$ 的正整数成立．对于正整数 $k$，记 $\displaystyle \overrightarrow{v}=\sum\limits_{i=2}^{2k}\overrightarrow{u_i}$，则由归纳假设，$|\overrightarrow{v}|\geqslant 1$，且 $\overrightarrow{v}$ 在 $\overrightarrow{u_2}$ 与 $\overrightarrow{u_{2k}}$ 之间，即在 $\angle P_{2k+1}OP_1$ 内．
设 $\overrightarrow{w}=\overrightarrow{u_1}+\overrightarrow{u_{2k+1}}$，则 $\displaystyle \overrightarrow{u}=\overrightarrow{v}+\overrightarrow{w}=\sum\limits_{i=1}^{2k+1}\overrightarrow{u_i}$．
当 $\overrightarrow{w}=\overrightarrow{0}$ 时，有 $|\overrightarrow{u}|=|\overrightarrow{v}|\geqslant 1$；当 $\overrightarrow{w}\ne\overrightarrow{0}$ 时，向量 $\overrightarrow{w}$ 平分角 $\angle P_1OP_{2k+1}$，因此 $\overrightarrow{w}$ 与 $\overrightarrow{u_1}$ 和 $\overrightarrow{u_{2k+1}}$ 的夹角小于 $\dfrac{\pi}{2}$，从而 $\overrightarrow{w}$ 与 $\overrightarrow{v}$ 的夹角小于 $\dfrac{\pi}{2}$，于是 $|\overrightarrow{u}|=|\overrightarrow{v}+\overrightarrow{w}|\geqslant |\overrightarrow{v}|\geqslant 1$，即命题对 $k$ 也成立．
从而命题对一切正奇数 $n$ 都成立．
答案
解析
备注
