空间中是否存在不在同一平面的有限点集 $M$,使得对 $M$ 中的任意两点 $A$ 和 $B$,我们可以在 $M$ 中另取 $C、D$ 两点,使直线 $AB$ 和 $CD$ 互相平行但不重合.(波兰)
【难度】
【出处】
1973年第15届IMO试题
【标注】
【答案】
略
【解析】
答案是肯定的.
构造例子如图所示.$M=\{A,B,C,D,E,F,G,H,P,Q\}$,其中 $ABCD-EFGH$ 为正方体,$P$ 为正方体的中心关于平面 $ADHE$ 的对称点,$Q$ 为正方体的中心关于平面 $BCGF$ 的对称点,则点集 $M$ 满足题设条件.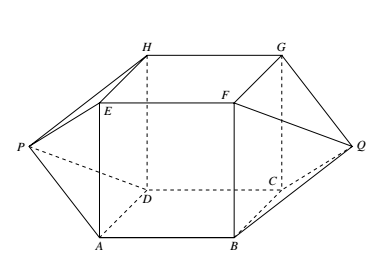
构造例子如图所示.$M=\{A,B,C,D,E,F,G,H,P,Q\}$,其中 $ABCD-EFGH$ 为正方体,$P$ 为正方体的中心关于平面 $ADHE$ 的对称点,$Q$ 为正方体的中心关于平面 $BCGF$ 的对称点,则点集 $M$ 满足题设条件.

答案
解析
备注