一个战士想要查遍一个正三角形区域内及边界上有无地雷，他的探测器的有效半径等于正三角形高的一半．这个战士从三角形的一个顶点出发开始探测．问他遵循这样的探测路线才能使查遍整个区域的路程最短？（南斯拉夫）
【难度】
【出处】
1973年第15届IMO试题
【标注】
【答案】
略
【解析】
设战士从顶点 $A$ 出发探测正三角形区域．$\triangle ABC$ 的高为 $2d$．以 $B$ 为圆心，$d$ 为半径作圆与 $AB,BC$ 分别交于 $M,N$；以 $C$ 为圆心，$d$ 为半径作圆与 $AC,BC$ 分别交于 $P,Q$．如图所示．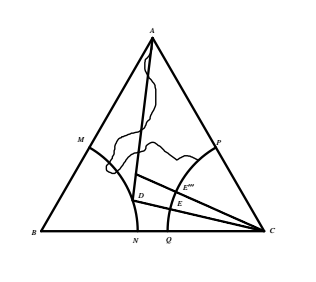
由题设，战士到达 $\overparen{MN}$ 上和 $\overparen{PQ}$ 上各至少一次．不妨设他先到达 $\overparen{MN}$ 上的 $D^\prime$ 后到达 $\overparen{PQ}$ 上的 $E^\prime$ 这两点．设 $D$ 为 $\overparen{MN}$ 中点．联结 $AD,CD,CD^\prime$ 分别与 $\overparen{PQ}$ 交于 $E,E^{\prime\prime}$．
不难看出，战士走过的路程 $\geqslant AD^\prime+D^\prime E^\prime\geqslant AD^\prime+D^\prime E^{\prime\prime}\geqslant AD+DE$．
最后一式是由于 $AD+DC\leqslant AD^\prime +D^\prime C^\prime$．这一点可简要说明如下：
过 $D$ 作切线 $l$ 平行于 $AC$，交 $AB,BC$ 分别与 $S,T$，则 $\angle ADS=\angle CDT$．由对称性知 $D$ 是 $l$ 上到 $A,C$ 距离之和最小的点．易见 $D^\prime $ 与 $C$ 在 $l$ 两侧．设 $CD^\prime$ 交 $l$ 于 $R$．则
$\begin{aligned}
AD+DC&\leqslant AR+RC\\
&\leqslant AD^\prime+D^\prime R+RC\\
&=AD^\prime+D^\prime C
\end{aligned}$
由于 $D$ 与 $AC$ 距离为 $d$，$AD$ 上任一点至 $AC$ 距离 $\leqslant d$，易知折线 $ADE$ 上的动点至 $AC$ 的垂线（$\leqslant d$）扫过四边形 $ADEF$（$EF\perp AC,F$ 是垂足，在扇形 $C$ 内）．至于 $\angle BAD$ 内，$\overparen{MN}$ 外的区域，以及 $DE$ 下面，两扇形外的区域，很容易验证其内任一点 $G$ 或 $G^\prime$，在 $AD$ 或 $DE$ 上必可找到点 $H$ 或 $H^\prime$，满足 $GH,G^\prime H^\prime<d$．因此 $ADE$ 就是最短路径，还有一条最短路径是先到 $\overparen{PQ}$ 后到 $\overparen{MN}$．
注意到 $\angle ABD=\angle CBD=30^\circ$，由余弦定理知最短路程为
$\begin{aligned}
&2\sqrt{\left(\dfrac{4}{\sqrt{3}d}\right)^2+d^2-\dfrac{8}{\sqrt{3}}d^2\cos 30^\circ}-d\\
&=\left(2\sqrt{\dfrac{7}{3}}-1\right)d\\
&=\dfrac{\sqrt{3}}{4}\left(2\sqrt{\dfrac{7}{3}}-1\right)AB\\
&=\left(\dfrac{\sqrt{7}}{2}-\dfrac{\sqrt{3}}{4}\right)AB
\end{aligned}$
由题设，战士到达 $\overparen{MN}$ 上和 $\overparen{PQ}$ 上各至少一次．不妨设他先到达 $\overparen{MN}$ 上的 $D^\prime$ 后到达 $\overparen{PQ}$ 上的 $E^\prime$ 这两点．设 $D$ 为 $\overparen{MN}$ 中点．联结 $AD,CD,CD^\prime$ 分别与 $\overparen{PQ}$ 交于 $E,E^{\prime\prime}$．不难看出，战士走过的路程 $\geqslant AD^\prime+D^\prime E^\prime\geqslant AD^\prime+D^\prime E^{\prime\prime}\geqslant AD+DE$．
最后一式是由于 $AD+DC\leqslant AD^\prime +D^\prime C^\prime$．这一点可简要说明如下：
过 $D$ 作切线 $l$ 平行于 $AC$，交 $AB,BC$ 分别与 $S,T$，则 $\angle ADS=\angle CDT$．由对称性知 $D$ 是 $l$ 上到 $A,C$ 距离之和最小的点．易见 $D^\prime $ 与 $C$ 在 $l$ 两侧．设 $CD^\prime$ 交 $l$ 于 $R$．则
$\begin{aligned}
AD+DC&\leqslant AR+RC\\
&\leqslant AD^\prime+D^\prime R+RC\\
&=AD^\prime+D^\prime C
\end{aligned}$
由于 $D$ 与 $AC$ 距离为 $d$，$AD$ 上任一点至 $AC$ 距离 $\leqslant d$，易知折线 $ADE$ 上的动点至 $AC$ 的垂线（$\leqslant d$）扫过四边形 $ADEF$（$EF\perp AC,F$ 是垂足，在扇形 $C$ 内）．至于 $\angle BAD$ 内，$\overparen{MN}$ 外的区域，以及 $DE$ 下面，两扇形外的区域，很容易验证其内任一点 $G$ 或 $G^\prime$，在 $AD$ 或 $DE$ 上必可找到点 $H$ 或 $H^\prime$，满足 $GH,G^\prime H^\prime<d$．因此 $ADE$ 就是最短路径，还有一条最短路径是先到 $\overparen{PQ}$ 后到 $\overparen{MN}$．
注意到 $\angle ABD=\angle CBD=30^\circ$，由余弦定理知最短路程为
$\begin{aligned}
&2\sqrt{\left(\dfrac{4}{\sqrt{3}d}\right)^2+d^2-\dfrac{8}{\sqrt{3}}d^2\cos 30^\circ}-d\\
&=\left(2\sqrt{\dfrac{7}{3}}-1\right)d\\
&=\dfrac{\sqrt{3}}{4}\left(2\sqrt{\dfrac{7}{3}}-1\right)AB\\
&=\left(\dfrac{\sqrt{7}}{2}-\dfrac{\sqrt{3}}{4}\right)AB
\end{aligned}$
答案
解析
备注
