求证：对整数 $n\geqslant 4$，每一个有外接圆的四边形，总可划分成 $n$ 个都有外接圆的四边形．（荷兰）
【难度】
【出处】
1972年第14届IMO试题
【标注】
【答案】
略
【解析】
若四边形是一等腰梯形，则可以用平行于底边的直线将它划分成 $n$ 个等腰梯形，因为任意一个等腰梯形都有外接圆，从而命题得证．
下设圆内接四边形 $ABCD$ 不是梯形，由于对角互补，不妨设 $\angle A\geqslant\angle C,\angle D\geqslant \angle B$，于是 $\angle A\geqslant\angle B,\angle D\geqslant \angle C$．
作 $\angle BAP=\angle B,\angle CDQ=\angle C$，且 $PQ\parallel AD$．再作 $PR\parallel AB$ 交 $BC$ 于 $R$，$QS\parallel DC$ 交 $BC$ 于 $S$，如图所示．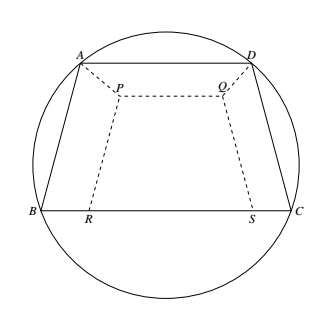
因为 $\angle DAP=\angle BAD-\angle ABC=(180^\circ-\angle BCD)-(180^\circ-\angle CDA)=\angle CDA-\angle BCD=\angle ADQ$，所以 $APQD$ 是等腰梯形．
四边形 $ABRP$ 和 $CDQS$ 都是等腰梯形．
又因为 $PQ\parallel AD,PR\parallel AB$，所以 $\angle QPR=\angle DAB$，由 $QS\parallel DC$ 知，$\angle RSQ=\angle BCD$，所以 $\angle QPR+\angle RSQ=\angle DAB+\angle BCD=180^\circ$，故四边形 $PQSR$ 有外接圆．
从上可知，我们把四边形划分成了 $4$ 个有外接圆的四边形，且其中有三个是等腰梯形，对于 $n>4$，我们可以进一步把其中的等腰梯形划分，使得恰好有 $n$ 个都有外接圆的四边形．
下设圆内接四边形 $ABCD$ 不是梯形，由于对角互补，不妨设 $\angle A\geqslant\angle C,\angle D\geqslant \angle B$，于是 $\angle A\geqslant\angle B,\angle D\geqslant \angle C$．
作 $\angle BAP=\angle B,\angle CDQ=\angle C$，且 $PQ\parallel AD$．再作 $PR\parallel AB$ 交 $BC$ 于 $R$，$QS\parallel DC$ 交 $BC$ 于 $S$，如图所示．
因为 $\angle DAP=\angle BAD-\angle ABC=(180^\circ-\angle BCD)-(180^\circ-\angle CDA)=\angle CDA-\angle BCD=\angle ADQ$，所以 $APQD$ 是等腰梯形．四边形 $ABRP$ 和 $CDQS$ 都是等腰梯形．
又因为 $PQ\parallel AD,PR\parallel AB$，所以 $\angle QPR=\angle DAB$，由 $QS\parallel DC$ 知，$\angle RSQ=\angle BCD$，所以 $\angle QPR+\angle RSQ=\angle DAB+\angle BCD=180^\circ$，故四边形 $PQSR$ 有外接圆．
从上可知，我们把四边形划分成了 $4$ 个有外接圆的四边形，且其中有三个是等腰梯形，对于 $n>4$，我们可以进一步把其中的等腰梯形划分，使得恰好有 $n$ 个都有外接圆的四边形．
答案
解析
备注
