给定 $4$ 个不重合的互相平行的平面，试证：存在一个正四面体，它的 $4$ 个顶点分别在这 $4$ 个平面上．（英国）
【难度】
【出处】
1972年第14届IMO试题
【标注】
【答案】
略
【解析】
如图，设这 $4$ 个平面依次为 $E_1,E_2,E_3,E_4$，记平面 $E_i$ 与平面 $E_{i+1}$ 间的距离为 $d_i(i=1,2,3)$．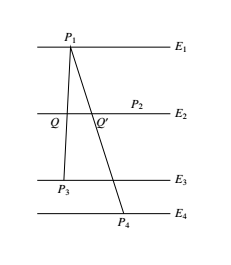
假定有一个四面体 $P_1P_2P_3P_4,P_i$ 落在 $E_i$ 内，设 $P_1P_3,P_1P_4$ 分别交平面 $E_2$ 于 $Q,Q^\prime$．
易知有 $\dfrac{P_1Q}{P_3Q}=\dfrac{d_1}{d_2},\dfrac{P_1Q^\prime}{P_4Q^\prime}=\dfrac{d_1}{d_2+d_3}$．
$P_2,Q,Q^\prime$ 不共线，可确定一平面．
于是，可这样解题．
先寻找一正四面体，不妨设为 $P_1^\prime P_2^\prime P_3^\prime P_4^\prime$，在 $P_1^\prime P_3^\prime$ 和 $P_1^\prime P_4^\prime$ 上分别找点 $Q_1$ 和 $Q_1^\prime$，满足 $\dfrac{P_1^\prime Q}{P_3^\prime Q}=\dfrac{d_1}{d_2},\dfrac{P_1^\prime Q_1^\prime}{P_4^\prime Q_1^\prime}=\dfrac{d_1}{d_2+d_3}$，作平面 $E_2^\prime$ 过 $P_2^\prime$ 和 $Q_1$，$Q_1^\prime$，再作平面 $E^\prime_1,E_3^\prime,E_4^\prime$，使其均平行于 $E_2^\prime$，并分别过 $P_1^\prime,P_3^\prime,P_4^\prime$．
设 $E_i^\prime$ 与 $E_{i+1}^\prime$ 之间的距离为 $d_i^\prime(i=1,2,3)$，易知 $d_1^\prime:d_2^\prime:d_3^\prime=d_1:d_2:d_3$，即诸 $E_i^\prime(i=1,2,3,4)$ 与诸 $E_i(i=1,2,3,4)$ 是相似的．
再让 $E_1$ 与 $E_1^\prime$ 重合，$P_i^\prime$ 与 $E_j$，$E_j^\prime$ 在 $E_1$ 同侧 $(2\leqslant i,j\leqslant 4)$，$P_1\prime$ 不妨设为 $P_1$，在射线 $P_1P_2^\prime,P_1P_3^\prime,P_1P_4^\prime$ 上分别找点（不妨设为 $P_2,P_3,P_4$），满足 $P_1P_2:P_1P_2^\prime=P_1P_3:P_1P_3^\prime=P_1P_4:P_1P_4^\prime=d_1:d_1^\prime$．易知四面体 $P_1P_2P_3P_4$ 为正四面体，且 $P_i$ 落在 $E_i(i=1,2,3,4)$ 上．
假定有一个四面体 $P_1P_2P_3P_4,P_i$ 落在 $E_i$ 内，设 $P_1P_3,P_1P_4$ 分别交平面 $E_2$ 于 $Q,Q^\prime$．易知有 $\dfrac{P_1Q}{P_3Q}=\dfrac{d_1}{d_2},\dfrac{P_1Q^\prime}{P_4Q^\prime}=\dfrac{d_1}{d_2+d_3}$．
$P_2,Q,Q^\prime$ 不共线，可确定一平面．
于是，可这样解题．
先寻找一正四面体，不妨设为 $P_1^\prime P_2^\prime P_3^\prime P_4^\prime$，在 $P_1^\prime P_3^\prime$ 和 $P_1^\prime P_4^\prime$ 上分别找点 $Q_1$ 和 $Q_1^\prime$，满足 $\dfrac{P_1^\prime Q}{P_3^\prime Q}=\dfrac{d_1}{d_2},\dfrac{P_1^\prime Q_1^\prime}{P_4^\prime Q_1^\prime}=\dfrac{d_1}{d_2+d_3}$，作平面 $E_2^\prime$ 过 $P_2^\prime$ 和 $Q_1$，$Q_1^\prime$，再作平面 $E^\prime_1,E_3^\prime,E_4^\prime$，使其均平行于 $E_2^\prime$，并分别过 $P_1^\prime,P_3^\prime,P_4^\prime$．
设 $E_i^\prime$ 与 $E_{i+1}^\prime$ 之间的距离为 $d_i^\prime(i=1,2,3)$，易知 $d_1^\prime:d_2^\prime:d_3^\prime=d_1:d_2:d_3$，即诸 $E_i^\prime(i=1,2,3,4)$ 与诸 $E_i(i=1,2,3,4)$ 是相似的．
再让 $E_1$ 与 $E_1^\prime$ 重合，$P_i^\prime$ 与 $E_j$，$E_j^\prime$ 在 $E_1$ 同侧 $(2\leqslant i,j\leqslant 4)$，$P_1\prime$ 不妨设为 $P_1$，在射线 $P_1P_2^\prime,P_1P_3^\prime,P_1P_4^\prime$ 上分别找点（不妨设为 $P_2,P_3,P_4$），满足 $P_1P_2:P_1P_2^\prime=P_1P_3:P_1P_3^\prime=P_1P_4:P_1P_4^\prime=d_1:d_1^\prime$．易知四面体 $P_1P_2P_3P_4$ 为正四面体，且 $P_i$ 落在 $E_i(i=1,2,3,4)$ 上．
答案
解析
备注
