四面体 $ABCD$ 的各面都是锐角三角形，考察所有的多边形 $XYZTX$，其中 $X,Y,Z,T$ 分别是 $AB,BC,CD,DA$ 的内分点，试证：
（$a$）若 $\angle DAB+\angle BCD\not=\angle CDA+\angle ABC$，那么不存在周长最小的多边形 $XYZTX$．
（$b$）若 $\angle DAB+\angle BCD=\angle CDA+\angle ABC$，那么存在无限多个周长最小的多边形 $XYZTX$，且其周长为 $2AC\sin \dfrac{\alpha }{2}$，这里 $α=\angle BAC+\angle CAD+\angle DAB$．（荷兰）
（$a$）若 $\angle DAB+\angle BCD\not=\angle CDA+\angle ABC$，那么不存在周长最小的多边形 $XYZTX$．
（$b$）若 $\angle DAB+\angle BCD=\angle CDA+\angle ABC$，那么存在无限多个周长最小的多边形 $XYZTX$，且其周长为 $2AC\sin \dfrac{\alpha }{2}$，这里 $α=\angle BAC+\angle CAD+\angle DAB$．（荷兰）
【难度】
【出处】
1971年第13届IMO试题
【标注】
【答案】
略
【解析】
（$a$）如图，将四面体 $ABCD$ 的四个面在平面上展开．（本来 $A$ 与 $A_1$，$D$ 与 $D_1$ 重合）易知有 $CA_1=CA,BD_1=BD,A_1D_1=AD$．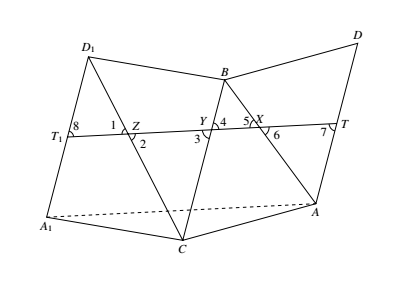
考虑折线 $XYZ$，如 $Y$ 不在 $XZ$ 上，则 $XY+YZ>XZ$，而由于 $\triangle ABC,\triangle BCD_1$ 都是锐角三角形，$XZ$ 与 $BC$ 必定相交，设为 $Y^\prime$，则用 $Y^\prime $ 代替 $Y$，可得 $XY^\prime ZTX$ 有更小周长，于是，若 $XYZTX$ 有最小周长，其展开必定是直的，即线段 $TT_1$．
由于 $\angle 1=\angle 2,\angle 3=\angle 4,\angle 5=\angle 6$，只要在 $A_1D_1$ 左侧补上 $\triangle ADB$ 即知 $\angle 7=\angle 8$，于是
$\begin{aligned}
\angle DAB+\angle BCD_1&=360^\circ-(\angle 2+\angle 3+\angle 6+\angle 7)\\
&=360^\circ-(\angle 4+\angle 5+\angle 1+\angle 8)\\
&=\angle ABC+\angle A_1D_1C_1
\end{aligned}$ ①
回到原来的四面体，① 式就是 $\angle DAB+\angle BCD=\angle ABC+\angle ADC$．
因此局部调整告诉我们（$a$）得证．
（b）易知 $A_1T_1=AT,AD\parallel A_1D_1$，故四边形 $ATT_1A_1$ 是平行四边形，于是 $TT_1=AA_1=2AC\sin\dfrac{\angle ACA_1}{2}$．而
$\begin{aligned}
\angle ACA_1&=\angle ACB+\angle BCD_1+\angle A_1CD_1\\
&=\angle 4+\angle 5-\angle BAC+180^\circ-\angle 2-\angle 3+\angle 1+\angle 8-\angle CA_1D_1\\
&=\angle 5+\angle 8-\angle BAC-\angle CA_1D_1+180^\circ\\
&=\angle 6+\angle 7 -\angle BAC-\angle CA_1D_1+180^\circ\\
&=360^\circ-(\angle BAD+\angle BAC+\angle CA_1D_1)\\
&=360^\circ-\alpha
\end{aligned}$
于是，$XYZTX$ 的最小周长为 $2AC\sin(180^\circ-\dfrac{\alpha}{2})=2AC\sin\dfrac{\alpha}{2}$．
由 $AT$ 的可伸缩性，可知这样的四边形有无限多个．
考虑折线 $XYZ$，如 $Y$ 不在 $XZ$ 上，则 $XY+YZ>XZ$，而由于 $\triangle ABC,\triangle BCD_1$ 都是锐角三角形，$XZ$ 与 $BC$ 必定相交，设为 $Y^\prime$，则用 $Y^\prime $ 代替 $Y$，可得 $XY^\prime ZTX$ 有更小周长，于是，若 $XYZTX$ 有最小周长，其展开必定是直的，即线段 $TT_1$．由于 $\angle 1=\angle 2,\angle 3=\angle 4,\angle 5=\angle 6$，只要在 $A_1D_1$ 左侧补上 $\triangle ADB$ 即知 $\angle 7=\angle 8$，于是
$\begin{aligned}
\angle DAB+\angle BCD_1&=360^\circ-(\angle 2+\angle 3+\angle 6+\angle 7)\\
&=360^\circ-(\angle 4+\angle 5+\angle 1+\angle 8)\\
&=\angle ABC+\angle A_1D_1C_1
\end{aligned}$ ①
回到原来的四面体，① 式就是 $\angle DAB+\angle BCD=\angle ABC+\angle ADC$．
因此局部调整告诉我们（$a$）得证．
（b）易知 $A_1T_1=AT,AD\parallel A_1D_1$，故四边形 $ATT_1A_1$ 是平行四边形，于是 $TT_1=AA_1=2AC\sin\dfrac{\angle ACA_1}{2}$．而
$\begin{aligned}
\angle ACA_1&=\angle ACB+\angle BCD_1+\angle A_1CD_1\\
&=\angle 4+\angle 5-\angle BAC+180^\circ-\angle 2-\angle 3+\angle 1+\angle 8-\angle CA_1D_1\\
&=\angle 5+\angle 8-\angle BAC-\angle CA_1D_1+180^\circ\\
&=\angle 6+\angle 7 -\angle BAC-\angle CA_1D_1+180^\circ\\
&=360^\circ-(\angle BAD+\angle BAC+\angle CA_1D_1)\\
&=360^\circ-\alpha
\end{aligned}$
于是，$XYZTX$ 的最小周长为 $2AC\sin(180^\circ-\dfrac{\alpha}{2})=2AC\sin\dfrac{\alpha}{2}$．
由 $AT$ 的可伸缩性，可知这样的四边形有无限多个．
答案
解析
备注
