设点 $M$ 是 $\triangle ABC$ 的 $AB$ 边上任一内点，${r}_{1},{r}_{2},r$ 分别是 $\triangle AMC,\triangle BMC,\triangle ABC$ 的内切圆半径：$q_1,q_2,q$ 分别是上述这些三角形在 $\angle ACM,\angle BCM,\angle ACB$ 内的旁切圆半径．试证：$\dfrac{{{r}_{1}}}{{{q}_{1}}}\cdot \dfrac{{{r}_{2}}}{{{q}_{2}}}=\dfrac{r}{q}$．（波兰）
【难度】
【出处】
1970年第12届IMO试题
【标注】
【答案】
略
【解析】
如图，设 $\triangle AMC$ 的内切圆圆心和旁切圆圆心分别为 $O_1,O^\prime_1$；$\triangle CMB$ 的内切圆圆心和旁切圆圆心分别为 $O_2,O^\prime_2$．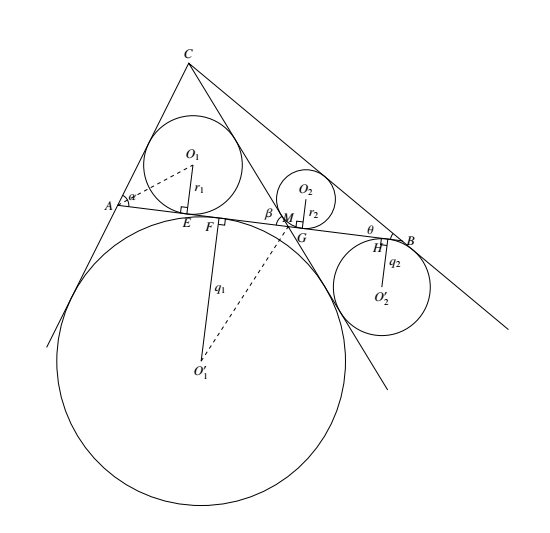
$O_1,O_1^\prime,O_2,O_2^\prime$ 在 $AB$ 上的射影分别为 $E,F,G,H$．
又设 $\angle CAB=\alpha,\angle CBA=\beta,\angle AMC=\theta,\angle CMB=180^\circ-\theta$．联结 $O_1A,MO_1^\prime$．
易知 $AE=MF=\dfrac{1}{2}(AC+AM-MC)$．
而 $\begin{aligned}
AE&=O_1E\cot\dfrac{\alpha}{2}=r_1\cot\dfrac{\alpha}{2}\\
MF&=O_1^\prime F\cot\dfrac{180^\circ-\theta}{2}\\
&=q_1\tan\dfrac{\theta}{2}
\end{aligned}$
因此，$\dfrac{r_1}{q_1}=\tan\dfrac{\alpha}{2},\tan\dfrac{\theta}{2}$，同理
$\begin{aligned}
\dfrac{r_2}{q_2}&=\tan\dfrac{\beta}{2}\tan\dfrac{180^\circ-\theta}{2}\\
&=\tan\dfrac{\beta}{2}\cot\dfrac{\theta}{2}\\
\dfrac{r}{q}&=\tan\dfrac{\alpha}{2}\cot\dfrac{\beta}{2}\\
\end{aligned}$
于是 $\dfrac{r_1}{q_1}\cdot\dfrac{r_2}{q_2}=\dfrac{r}{q}$．
$O_1,O_1^\prime,O_2,O_2^\prime$ 在 $AB$ 上的射影分别为 $E,F,G,H$．又设 $\angle CAB=\alpha,\angle CBA=\beta,\angle AMC=\theta,\angle CMB=180^\circ-\theta$．联结 $O_1A,MO_1^\prime$．
易知 $AE=MF=\dfrac{1}{2}(AC+AM-MC)$．
而 $\begin{aligned}
AE&=O_1E\cot\dfrac{\alpha}{2}=r_1\cot\dfrac{\alpha}{2}\\
MF&=O_1^\prime F\cot\dfrac{180^\circ-\theta}{2}\\
&=q_1\tan\dfrac{\theta}{2}
\end{aligned}$
因此，$\dfrac{r_1}{q_1}=\tan\dfrac{\alpha}{2},\tan\dfrac{\theta}{2}$，同理
$\begin{aligned}
\dfrac{r_2}{q_2}&=\tan\dfrac{\beta}{2}\tan\dfrac{180^\circ-\theta}{2}\\
&=\tan\dfrac{\beta}{2}\cot\dfrac{\theta}{2}\\
\dfrac{r}{q}&=\tan\dfrac{\alpha}{2}\cot\dfrac{\beta}{2}\\
\end{aligned}$
于是 $\dfrac{r_1}{q_1}\cdot\dfrac{r_2}{q_2}=\dfrac{r}{q}$．
答案
解析
备注
