设在四面体 $ABCD$ 中，$\angle BDC$ 是直角，$D$ 到平面 $ABC$ 的垂足 $S$ 是 $\triangle ABC$ 的垂心．试证：${(AB+BC+CA)}^{2}\leqslant 6({AD}^{2}+{BD}^{2}+{CD}^{2})$．并说明等号成立时是一个什么四面体？（保加利亚）
【难度】
【出处】
1970年第12届IMO试题
【标注】
【答案】
略
【解析】
如图，$DS\perp $ 平面 $ABC$，故 $DS\perp AC$．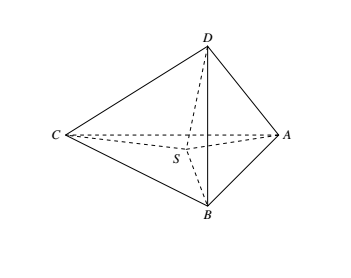
又 $BS\perp AC$，所以 $BD\perp AC$，又 $BD\perp CD$，故 $BD\perp $ 平面 $ADC$，所以 $BD\perp AD,\angle ADB=90^\circ$，同理 $\angle ADC=90^\circ$．
由勾股定理，得
$\begin{aligned}
AB^2&=AD^2+BD^2\\
BC^2&=BD^2+CD^2\\
CA^2&=CD^2+AD^2
\end{aligned}$
利用柯西不等式（或算术-几何平均不等式），得
$(AB+BC+CA)^2\leqslant 3(AB^2+BC^2+CA^2)=6(AD^2+BD^2+CD^2)$
等号成立，必须有 $AB=BC=CA$，由此推得 $AD=BD=CD$．此时 $\triangle ABD,\triangle ACD,\triangle BCD$ 均为等腰直角三角形，$\triangle ABC$ 为一正三角形．
又 $BS\perp AC$，所以 $BD\perp AC$，又 $BD\perp CD$，故 $BD\perp $ 平面 $ADC$，所以 $BD\perp AD,\angle ADB=90^\circ$，同理 $\angle ADC=90^\circ$．由勾股定理，得
$\begin{aligned}
AB^2&=AD^2+BD^2\\
BC^2&=BD^2+CD^2\\
CA^2&=CD^2+AD^2
\end{aligned}$
利用柯西不等式（或算术-几何平均不等式），得
$(AB+BC+CA)^2\leqslant 3(AB^2+BC^2+CA^2)=6(AD^2+BD^2+CD^2)$
等号成立，必须有 $AB=BC=CA$，由此推得 $AD=BD=CD$．此时 $\triangle ABD,\triangle ACD,\triangle BCD$ 均为等腰直角三角形，$\triangle ABC$ 为一正三角形．
答案
解析
备注
